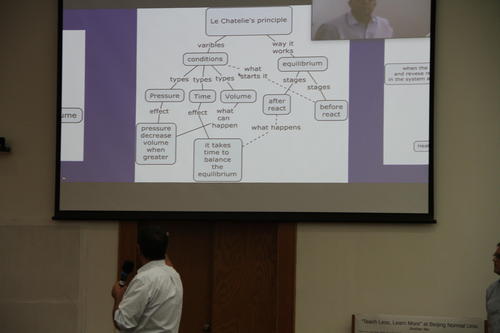
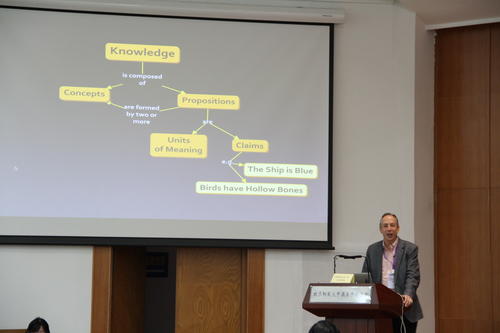
In order to stimulate, provoke and inspire more to think about what to teach/learn and how to teach/learn and also to learn for understanding for the world and ourselves, we held The First Asian Pacific Conference on Concept Mapping during 20-22/09, 2017 at Beijing Normal University. Before the full and officially published proceeding can be released to all the participants and also to the public, in the following I will provide links to the photos and documents of the presented talks. These are only a part of all the photos and presentations, which will be updated to this website in the next few days and also will be post on IHMC website later on.
I would like to take this opportunity to thank all the organizers again for their hard work and also thank all of you participants for all the questions, discussions, presentations, and encouragement. Without the great support from all of you, there is no CMC-AP 2017.
为了刺激、挑战和启发更多人来思考教什么怎么教,学什么怎么学,为了让教育向着为了理解世界和自我而学习,我们在9月20-22日于北京师范大学召开了“亚太地区概念地图大会”。在大会正式的印刷版的文集出来之前,我在这里提供照片和报告文档的下载。这些材料现在还不完整。将来会更加完整。也会不久之后在IHMC的网站上发布。
借这个机会,我想再次表达我的衷心感谢,谢谢所有的组织者的辛劳,谢谢所有的参会者贡献的问题、讨论、报告以及鼓励。没有你们的支持,就没有这个会议。
会议文集(Proceeding)
会议报告文档(Program and Presentations)
| 9月20日 | ||||
| 时间(Time) | 报告类型(Type) | 主题(Title) | 主讲人(Speaker) | 主持人(Chairperson) |
| 07:20-08:15 | Registration(报到) | |||
| 08:15-08:30 | Welcome message from BNU President (北京师范大学校长致欢迎辞) | Jinshan Wu | ||
| 08:30-09:15 | Welcome message and presentation from Joseph Novak(Joseph Novak致欢迎辞及陈述发言) | |||
| 09:15-09:30 | Photo | |||
| 09:30-10:30 | Invited | Using concept mapping to develop theory in educational research(利用概念地图发展教育研究理论) | Ian Kinchin | |
| 10:30-10:45 | Tea Break | |||
| 10:45-11:30 | Research | Analysing curriculum design conceptual frameworks(分析课程设计概念框架) | Cherry Stewart | Ian Kinchin |
| 11:30-11:45 | Innovative | Knowledge Elicitation and Mapping in Cynefin Framework(库尼文架构中的知识启发和地图制作) | Haley Wing Chi Tsang | |
| 11:45-12:00 | Innovative | Examining Students’ Attitude Toward Thinking and Learning in Computer-Assisted Concept Mapping among Undergraduate Thinking Skills Class(考察学生对计算机思考和学习的态度-本科思维技能课程的辅助概念地图) | Sui Chong Nicholas Ling | |
| 12:00-14:00 | Lunch | |||
| 14:00-15:00 | Invited | Assessment with and of Concept Maps(概念地图的评估及使用概念地图做评估) | Priit Reiska | Alberto Cañas |
| 15:00-15:45 | Research | Comparing different assessment methods for measuring students’ biology knowledge(比较测量学生的生物学知识的不同评估方法) | Aet Möllits* | |
| 15:45-16:00 | Tea Break | |||
| 16:00-16:45 | Research | The effects of concept mapping on learning performances and self-efficacy for college students(概念構圖對大學生學習成效與自我效能的影響) | Yu-Ju Chang | Jinxin Hao |
| 16:45-17:00 | Innovative | The influence of art education on children’s painting activities by using Concept Map(利用概念图的美术教育对儿童绘画活动的影响) | 黄悦欣 Yuexin Huang | |
| 17:00-17:15 | Innovative | Exploring the application of Concept Maps on Moral Education in junior middle school- Take "A Basic Economic System full of Vitality and Vitality" as an example(概念图应用于初中思想品德教学的探索 —以《充满生机和活力的基本经济制度》为例) | 李晓杰 Xiaojie Li | |
| 18:00 | Dinner | |||
| 9月21日 | ||||
| 时间(Time) | 报告类型(Type) | 主题(Title) | 主讲人(Speaker) | 主持人(Chairperson) |
| 08:30-09:30 | Invited | Using Concept Mapping to Develop Higher-Order Thinking Skills(使用概念地图来开发更高层次的思考技能) | Alberto J. Cañas | Hui-Ying Ho |
| 09:30-10:15 | Research | concept mapping As A pre-writing strategy on EFL high school students’ English writing(概念地图作为高中学生英语写作的写作前策略) | 陈钱钱 Qianqian Chen* | |
| 10:15-10:30 | Innovative | Build a graphics connection and develop students’ thinking(构建图形联系,发展学生思维) | 薛冬 Dong Xue* | |
| 10:30-10:45 | Tea Break | |||
| 10:45-11:45 | Panel discussion(大会讨论) | Concept mapping in your work(概念地图的使用) | Ian, Priit, Alberto, Jinshan and all participants | Michael Brody |
| 11:45-12:00 | Innovative | Concept Mapping Note Taking and the Production of Educative Hypermedia for the Graduate student(概念地图绘制笔记和供给研究生的教育超媒体) | Manuel F. Aguilar-Tamayo | |
| 12:00-14:00 | Lunch | |||
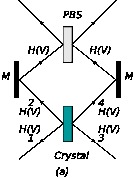
| 14:00-15:00 | Invited | Designing the K-12 Teaching Modulus of Photonic Crystal and Lotus Effect via Concept Maps(通过概念地图设计光子晶体和莲花效应的基础教育教学模型) | Huei-Ying Ho | Hsiao-Ping Yu |
| 15:00-15:45 | Research | The Role of Concept Maps in the Improvement of the Teaching and Learning Process(概念地图在教学和学习过程改进中的作用) | Liberato Cardellini | |
| 15:45-16:00 | Tea Break | |||
| 16:00-16:45 | Research | Concept Mapping as an Assessment of Cognitive Load and Mental effort in Complex Problem Solving in chemistry(概念地图作为在化学复杂问题解决中的认知负荷和脑力劳动的评估) | Michael Brody | Charles (Kip) Ault |
| 16:45-17:00 | Innovative | READING WITH MYTHOSLITE: EVALUATING AN E-ANNOTATIONS FOR HOMER’S THE ILIAD AND THE ODYSSEY(使用MythosLite阅读:评估荷马的《伊利亚特》和《奥德赛》的电子注释) | Ai Chun Yen * | |
| 17:00-18:00 | Invited | Implementation and Effect of Using Concept Mapping to Teach the Gifted Students(资优生概念地图教学之实施与成效探究) | Hsiao-Ping Yu | |
| 18:00 | Poster and Dinner | |||
| 9月22日 | ||||
| 时间(Time) | 报告类型(Type) | 主题(Title) | 主讲人(Speaker) | 主持人(Chairperson) |
| 08:30-09:30 | Invited | "Teach Less, Learn More" at Beijing Normal University(以概念地图为基础的理解型学习在北京师范大学) | 吴金闪 Jinshan Wu | Priit Reiska |
| 09:30-10:15 | Research | THINKING GEOLOGIC THOUGHTS: INTERPRETING TRACES OF PAST EVENTS(思考地质思想:解释过去事件的痕迹) | Charles R. Ault | |
| 10:15-10:30 | Innovative | Using Concept Mapping to Identify Key Ideas in the Development of a K-9 Computational Thinking(使用概念地图来识别k-9计算思维的发展中的关键思想) | Alberto J. Cañas | |
| 10:30-10:45 | Tea Break | |||
| 10:45-11:00 | Innovative | Destination Image Concept Mapping based on Frame Analysis(基于框架分析的旅游目的地形象概念构图研究) | 吴函雷 Hanlei Wu | Guoqing Zhao |
| 11:00-11:20 | Best Papers (2), Best Experiences (2) and Best Posters (2)(优秀论文(2),优秀经验(2),优秀海报(2)) | Best Papers and Best Experiences winners are marked with(优秀论文和优秀经验获得者标注了) * | Best Posters winners are(优秀海报获得者是): Maneesh Makheeja, Marcela Paz González-Brignardello | |
| 11:20-12:00 | Fairwell from Chair(告别会) | |||
| 12:00-14:00 | Lunch | |||
会议照片
如果你想下载照片,请左键点击照片,然后保存在新窗口打开的照片。请不要直接在本页面的照片上右击然后“另存为”,这样你只能得到一张解析度非常低的照片。
If you want to download a photo, please LEFT click on the photo and then save the photo that open up in the new browser window. Please do not RIGHT click the photo on this page and “save as”, that will only give you a very low resolution one.








































































































































































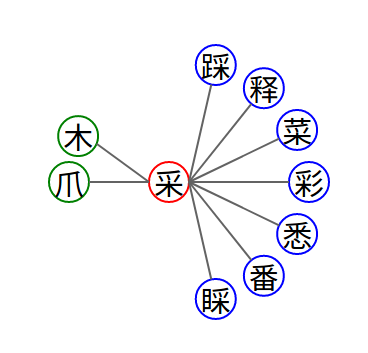
 。我不知道逸儿是不是能够把这个字通过这个书写笔画的过程想象出来,而且更进一步,就算能够想象出来,对于理解这个字有什么用。我说:逸儿,你知道木头的木吗?(回答“知道”)那就简单了,就是木头的木上面多了左右两点。它的含义就像是一个小禾苗或者小树木上面多了一点点小穗。见过长在地里的稻子吗?你知道米就是从那里来的。是不是像一个小禾苗或者小树木上面的穗子?通过这样的解释,逸儿把“米”和之前认识的字联系起来了,并且进一步通过联系生活实际,发现这样的联系还是有意义的,促进理解的。当然,实际上,按照甲骨文的字形,其本意看起来更像整个都代表的是小穗子(
。我不知道逸儿是不是能够把这个字通过这个书写笔画的过程想象出来,而且更进一步,就算能够想象出来,对于理解这个字有什么用。我说:逸儿,你知道木头的木吗?(回答“知道”)那就简单了,就是木头的木上面多了左右两点。它的含义就像是一个小禾苗或者小树木上面多了一点点小穗。见过长在地里的稻子吗?你知道米就是从那里来的。是不是像一个小禾苗或者小树木上面的穗子?通过这样的解释,逸儿把“米”和之前认识的字联系起来了,并且进一步通过联系生活实际,发现这样的联系还是有意义的,促进理解的。当然,实际上,按照甲骨文的字形,其本意看起来更像整个都代表的是小穗子(