-
前两天提到小学数学教材里面对于折线统计图的处理的错误:把给定(可能来自于统计)数据列表做出来折线图看做“折线统计图”。除了教材编写者没有考虑好什么是数学(用数学的眼光看世界和思考,把问题变成能够用数学形式思考的问题)之外,我说还是语文的问题。今天沿着这个思路再展开一下:根本上还是物理没学好的问题,没有运用好还原(不断把东西往下分割成小单元以及单元之间的联系)和综合(把分割好的东西以及这些东西之间的联系重新逐渐往上构建起来上层结构)。通过这个讨论,我还想说明,不管数学物理科学语文,它们都是一样的,就是多思考,尽量深入,还能够回来看到整体。顺便,这个思路有的时候,也叫作系统科学,或者系统思维。
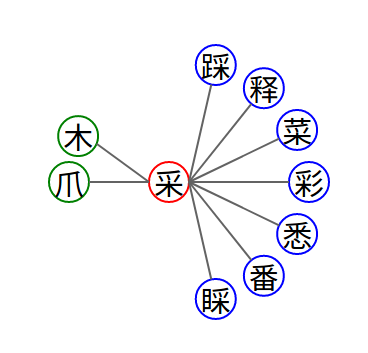
我们来看第一个例子。例如当我们需要教英语使用者中文的时候,比如就是“你好”这个词的含义,怎么办?整体认读和认知的时候,可以简单用“hello”来代表,或者,类似的“hi”。但是,其实这是不够的。更好的说法应该是“you (have a) good (day)”。更进一步,甚至可以和英文中的goodbye(原来代表“God be with you”,会面结束的时候常用的一句话,后来就引申为再见)联系起来。那为什么这样更好呢?因为了解“你好”的两个字分别代表“你——you”“好——good”对于学习汉语是有意义的。这个意义体现在两个方面。第一、这两个字分别可以构成其他的词语,例如“你们”、“好吃”。这时候学会单个字“你”和“好”的含义就可以迁移。也就是说,更小的结构会在其他地方出现。第二、组合是汉语的一大特点,因此,从具体例子来体会组合,是很好的一个学习汉语的方法。甚至,“汉语”和“方法”都是两个可以讲出来道理的词。更进一步,不仅仅是词,汉语的短语和句子也是组合形成的。
同样的道理,墨水的“墨”不能教到“ink”为止,需要更进一步。比如,可以解释成“black ash in water”,甚至进一步解释,墨实际上可以看做“黑”和“土”,其中“黑”就是指“火”(下面四个点的含义)上面方一个器皿得到的烟灰,也就是说,“墨”是“black ash, which often comes from smoking woods and is often what deposited on a cool plate over burning woods, in water”。想象一下这个时候,关于这个字的含义,学习者能够体会到多少,至少远远超过仅仅告诉学习者相当于“ink”。
我们再来看第二个例子。“折线统计图”是一个整体吗,还是“折线-统计-图”三个部分。当然,从语言本身来说,肯定是三个部分“折线-统计-图”,第一部分表示表示作图的类型,第二部分一个处理数据的过程,第三部分表示分析和作图得到的结果。甚至,我们还可以问语言上,“折线”是什么意思(一段段连起来的线段,不一定光滑),“统计”是什么意思(分类整合计数),“图”是什么意思。甚至,我们可以问为什么“统-计”两个字合起来是这个意思,甚至更加进一步“统”、“计”这两个字为什么分别是这个意思,原来是什么意思,如何把原来的意思迁移过来的,等等等等这样的问题。那我们为什么要这样做?因为“统计”还会用在除了“折线统计图”之外的其他地方,例如“柱状统计图”。当然,这是语文的角度。现在,我们来看数学的角度,“折线统计图”是一个必须整体认知的对象吗?不是。首先,我们可以对各种各样的数据,只要是已经成为两列的代表两个变量的数据,都做折线图分析。因此,折线图是独立于统计分析之外的东西。同样,统计分析也是独立于折线图之外的东西,完全可以统计完了不画折线图。因此,这两个概念是完全要分开的,也就是,学生应该学会“折线-统计-图”。
有了这两个例子,我们再回头来看,说明了什么问题。首先,学会所有的东西的过程中,都存在一个分解或者说还原到什么程度的问题。只有分解之后,独立出来的单元,将来才能在更多的场合发挥作用,成为进一步学习的基础。为什么医学研究着、化学家和物理学家需要把物质分解到分子甚至原子的层次?因为,例如在医学上一旦搞清楚了是某种分子在发挥某种作用,就可以有一个标准来制备这个药物,而不是仅仅通过某个特定的偶然发现的过程来制备,于是还可以用这个标准来检验。更进一步,可以把这个分子继续拆分,成为对应着某种功能的功能团等子结构,甚至进一步到原子的层次,问什么样的相互作用使得这些原子能够组合成具有这个特定功能的集团。了解了这个,就可以来做药物设计了。具体分解到哪一个层次和理解有关,也就是和下面要说的综合有关。其次,所谓的理解就是建立知识之间的联系,从已知知识到未知知识之间的联系,甚至已有概念之间的新的联系。例如,从数学概念上说,你可以把“折线图”特意取一个“柱状图”的名字,只要学术界保持一致,就没有问题。但是,这个时候,对于初次学习“折线图”的学习者来说,就很容易和日常生活中的“折线”的含义“错误地”联系起来。这也是为什么专有名词本身也经常在语言上是可以大概理解的。但是,仅仅是大概。有的时候,这样的联系,不一定对于理解这个概念是正面的,还需要放到专有名词的体系内部来建立联系。这个把分解完了的下层结构通过联系再次合起来的过程,就是综合。实际上,这是物理学的非常核心的典型思维方式之一。
在学习上,教学上,一定要做好这个分解和综合。一般来说,需要分解到一个层次,那个学习者认为完全理解了的层次,也就是通过考虑分解之后的各个部分的联系能够做到完全重新建立整体概念的层次。当然,好的学习者会一直追问,于是永远也不满足于某个中间的层次,一直到根本问题或者还没有答案的问题为止,甚至自己去探索这个未知的层次。不要满足于任何整体认知。没有深入到细节,则整体就是假象,觉得好像理解了;没有整体,只有细节,那就是迷途,没有方向(when there is no details, whole is delusional; when there is no whole, all is lost in details without sense of directions.)。






















































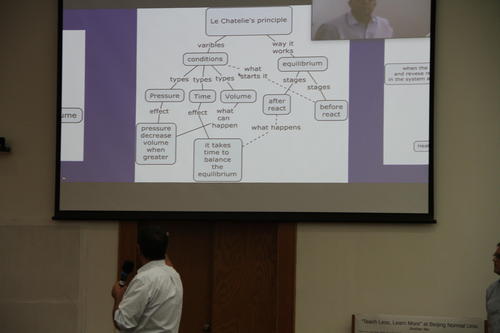





























































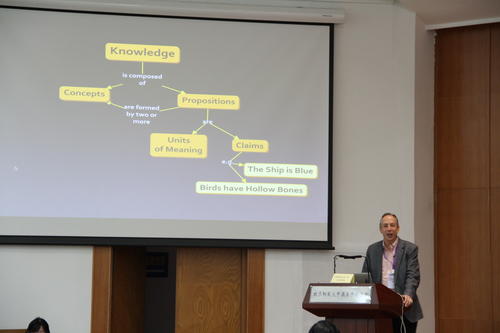


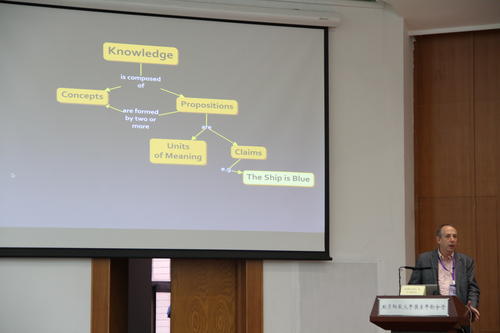



















































 。我不知道逸儿是不是能够把这个字通过这个书写笔画的过程想象出来,而且更进一步,就算能够想象出来,对于理解这个字有什么用。我说:逸儿,你知道木头的木吗?(回答“知道”)那就简单了,就是木头的木上面多了左右两点。它的含义就像是一个小禾苗或者小树木上面多了一点点小穗。见过长在地里的稻子吗?你知道米就是从那里来的。是不是像一个小禾苗或者小树木上面的穗子?通过这样的解释,逸儿把“米”和之前认识的字联系起来了,并且进一步通过联系生活实际,发现这样的联系还是有意义的,促进理解的。当然,实际上,按照甲骨文的字形,其本意看起来更像整个都代表的是小穗子(
。我不知道逸儿是不是能够把这个字通过这个书写笔画的过程想象出来,而且更进一步,就算能够想象出来,对于理解这个字有什么用。我说:逸儿,你知道木头的木吗?(回答“知道”)那就简单了,就是木头的木上面多了左右两点。它的含义就像是一个小禾苗或者小树木上面多了一点点小穗。见过长在地里的稻子吗?你知道米就是从那里来的。是不是像一个小禾苗或者小树木上面的穗子?通过这样的解释,逸儿把“米”和之前认识的字联系起来了,并且进一步通过联系生活实际,发现这样的联系还是有意义的,促进理解的。当然,实际上,按照甲骨文的字形,其本意看起来更像整个都代表的是小穗子(