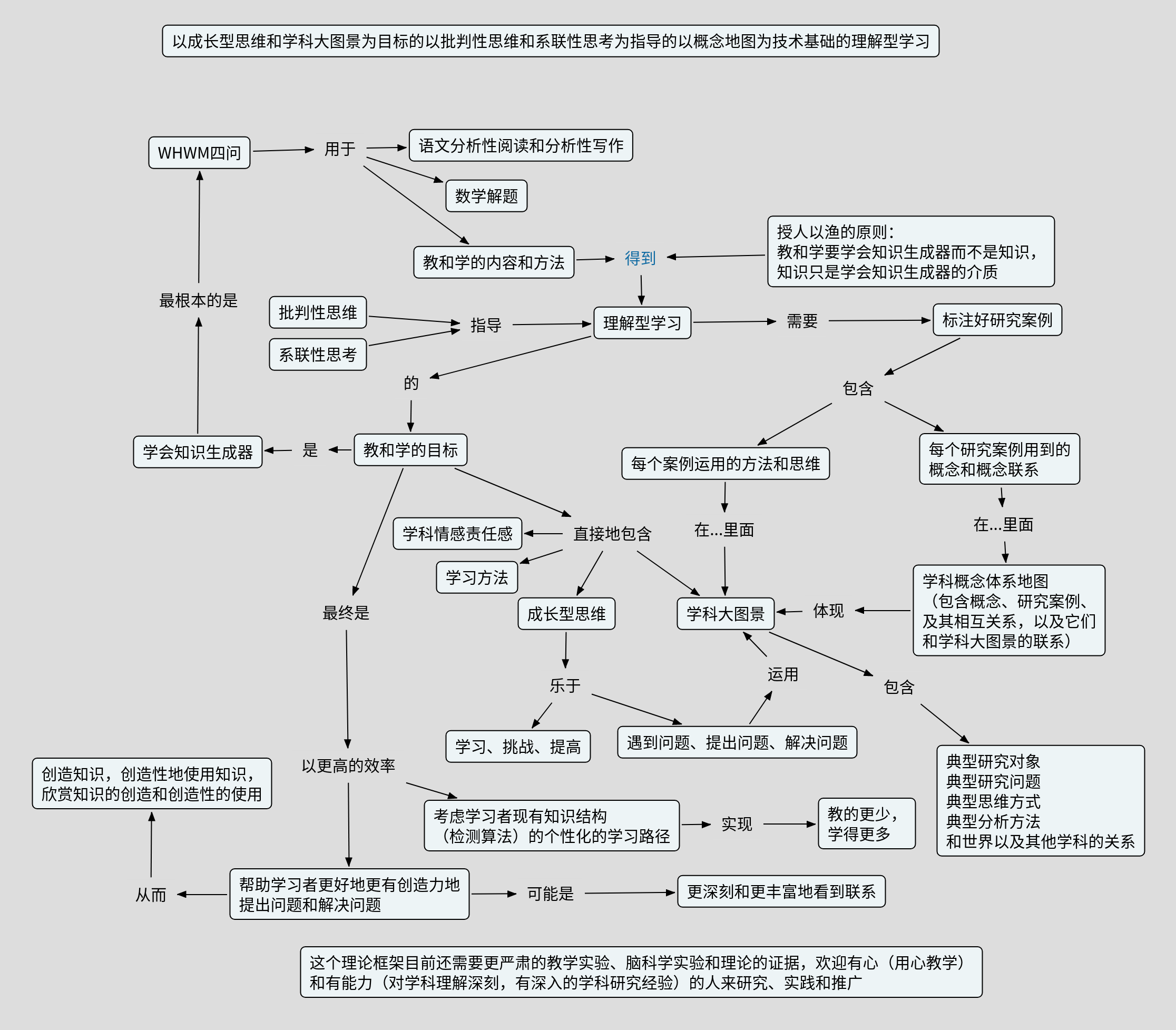
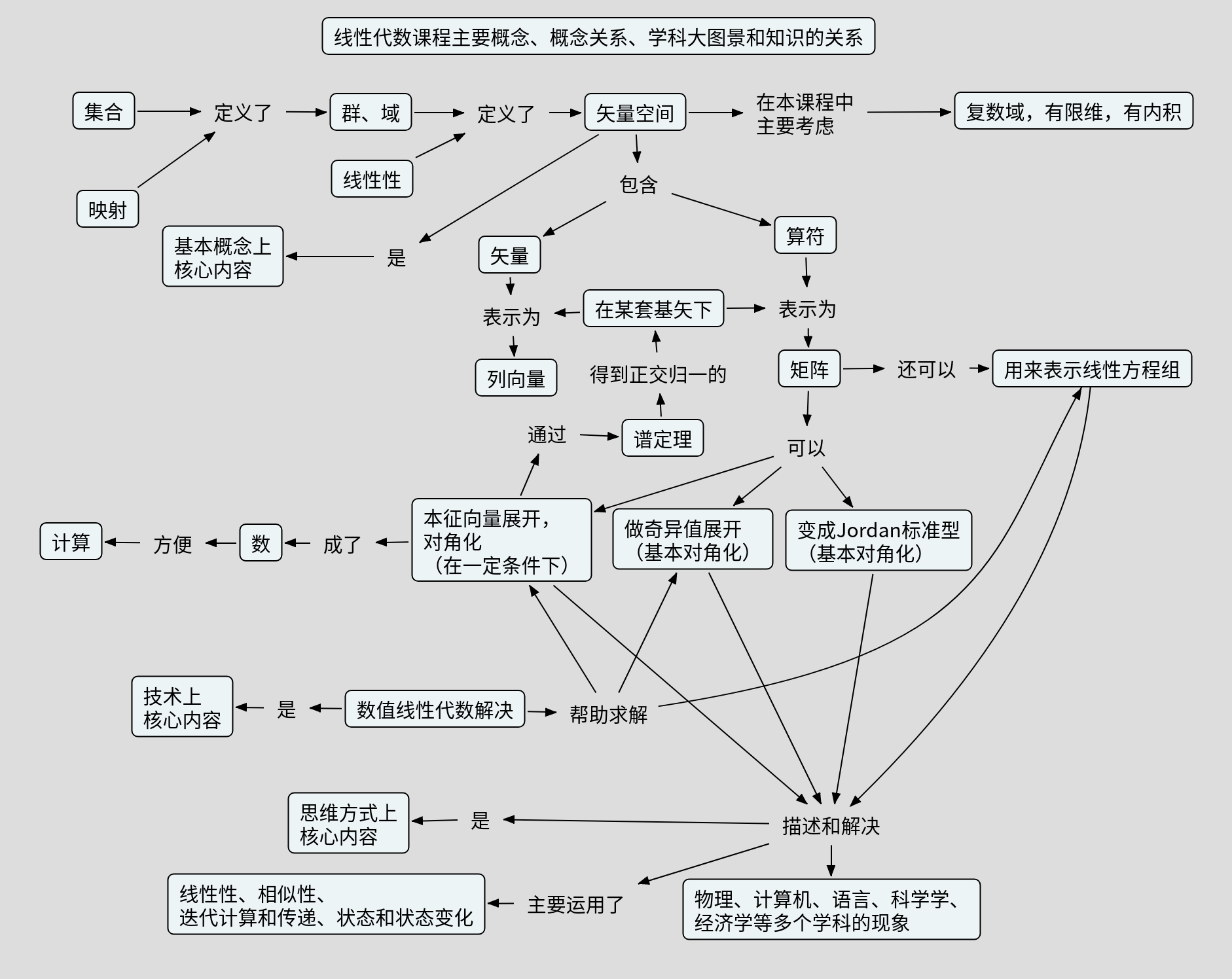
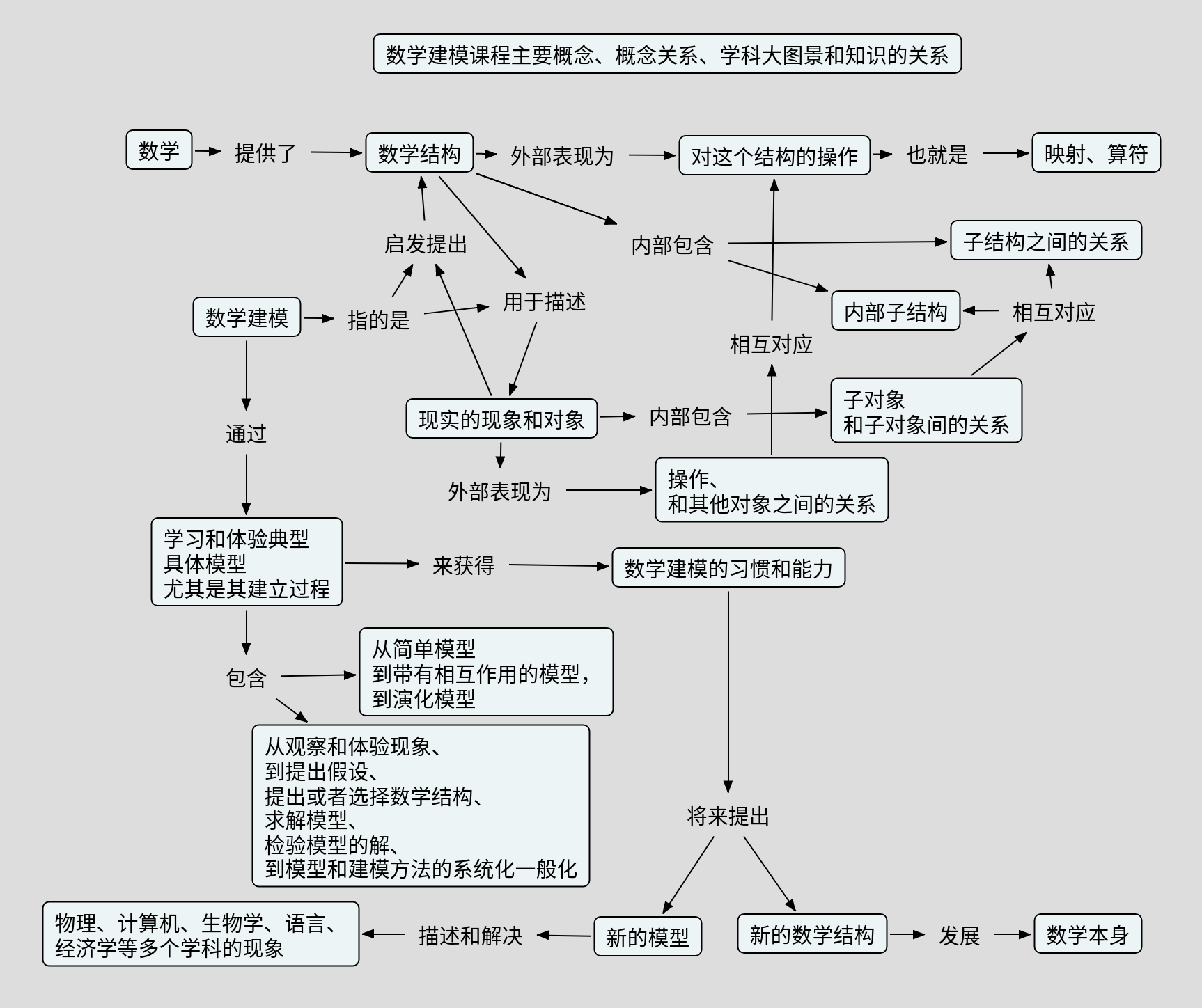
原来我们的WHWM方法是用在语文的分析性阅读和分析性写作上的,后来发现也可以用在数学解题上。今天,我们说,其实整个理解型学习也可以看做是这四个问题在教和学上的运用的结果。
理解型学习名词解释
先来补充一堆和理解型学习有关的名词的解释:
成长型思维:做中学、教中学、挑战着学、创造中学、任何时候都可以再进步。
学科大图景:一个学科的典型研究对象、典型研究问题、典型思维方式、典型分析方法、和世界还有其他学科的关系。学会知识还是创造学会知识的思想和方法(尽管,是不是其实这些思想和方法还是知识?),以科学为例——用具体例子体现科学是给世界构建一个可计算的心智模型并且这个模型给出来的结果和实验以及观测结果相符。如果是为了学会创造知识的方法,而不仅仅是知识,那么,学科大图景比知识本身重要。当然,不学习知识和知识的创造过程,体会不到学科大图景。
批判性思维:没有经过我自己的理性检验(观察实验或者计算推理)的东西不能成为我下一步思考和认识世界的基础。例如伽利略运用斜塔实验和纯思辨的理想实验对重物落得更快的批判以及我们对后者的批判、冰上运动和力是维持运动的原因。
系联性思考:未知联系已知就是理解,构建理解的基础和框架,具有系统性(核心和成长),和逐条记忆检索相反。注意,把联系表达成网络和矩阵之后,还可以分析和计算联系:系联=联系^1+联系^2+联系^3+…,从孤立到有联系,从直接联系到间接联系,从个体到整体。
概念地图:概念,通过联系,构成的网络。也称为知识图谱、概念网络。其中学科概念地图指的是把一个学科的主要概念、概念之间的关系、概念和学科大图景之间的关系,整理之后,制作出来的概念地图。
创造体验式学习,也称为创造中学、挑战着学:在学习新概念的时候,老师创设一个接近概念提出的当时的背景的问题,不管是从理论本身出发,还是从具体要解决的实际现象出发,启发学生把这个新概念自己创造出来,体验一下其创造过程,希望不仅能够帮助学生学会这个概念,还能迁移到如何创造其他类似概念。
以项目为基础的学习,也称为做中学:设计一个能够把之前学过的知识和思维方式用上的问题,或者选择一个类似的实际问题,来解决,从而帮助学生更好地理解学过的知识和思维方式。当这个项目用于启发学生“创造”新知识或者思维的时候,这就是创造体验式学习。
讲给别人听,或者叫同伴教学法,教中学:把一个问题给别人讲清楚,接受别人的提问和挑战,可以使得自己理解的更深刻更清楚。
教的更少,学得更多:在老师指导下,通过理解型学习、创造体验式学习等方式来学习尽可能少的核心概念和基本概念,以及依靠这些概念提出和运用过程来增加对一个学科的大图景的认知,从而自己学会创造知识、创造性地运用知识和进一步学习这个学科的知识,就实现了“教的更少,学得更多”的目的。
学的更少,学得更多:从学生的角度,可以在老师的指导下,也可以在合适的学习资料的帮助下自学,通过理解型学习、创造体验式学习等方式来学习尽可能少的核心概念和基本概念,以及依靠这些概念提出和运用过程来增加对一个学科的大图景的认知,从而自己学会创造知识、创造性地运用知识和进一步学习这个学科的知识,就实现了“学的更少,学得更多”的目的。
痛快教育:理解型学习、创造体验式学习的实践很多时候,会比主要依靠记忆和重复刷题的机械式学习更需要时间和思考的投入,这通常本身并不一定愉快,往往不轻松,但是学习以后的效果却往往会更快乐——学会了创造知识的方法、体验了创造的过程。把这个过程的痛和结果的快合起来称为“痛快教育”。专门选择了这样一个词来和“快乐教育”、“减负”对比起来。追求短期快乐,减掉思维负担的教育,长期来看,只能增加负担,增加痛苦。当然,如果减掉的不是思维负担,而是那些可有可无的知识点,可以被其他更好的知识点代替来体现学科大图景的知识点,那这个负是该减的。这样减掉之后就正好达到了“教的更少,学得更多”。然而,如果一位老师没有这些理念,或者对学科认识不够深刻,则减掉的往往就是思维负担,就是最重要的学科大图景,只留下一个个孤立的需要通过刷题来学习的知识点。
为了理解自己和世界而学习:看看世界到底怎么回事,这世界的哪些地方“我”自己竟然可以理解,看看我自己最善于做的是什么,为此而思考而学习而创造,是一件快乐而有意义的事情。
教和学的目的:学习的目的是创造知识,创造性地使用知识知识,欣赏知识的创造和创造性的使用。这一切的基础是对知识的理解,也就是构建起来有系统有层次的知识结构,对知识产生的过程以及过程中体现的学科大图景尤其是思维方式、分析方法的理解。教学的目的就是帮助学生实现上面的目标。例如,帮助学生学会学习方法和思考,包含理解型学习、创造体验式学习、以项目为基础的学习、讲给别人听、批判性思维、系联性思考等;提高学生通过学习和挑战来增加提出问题解决问题的能力的意愿,也就是培养成长型思维;培养学生从知识、研究案例知识提出的背景和过程的学习中体会好所在学科的学科大图景,包含典型问题、典型对象、典型思维方式、典型分析方法、和世界以及其他学科的关系,进而形成学科兴趣和责任感。
WHWM分析性阅读:What说了什么,How怎么说的,Why为什么说这个为什么这样说,Meaningful你觉得怎么样,对你来说读了以后意味着什么。
WHWM分析性写作:What我想说什么,How我想怎么说,Why我为什么说这个为什么这样说,Meaningful我预期我的读者会觉得怎么样,对它们来说读了以后意味着什么。
WHWM数学解题四问:What:算出来的和用来计算的东西是什么?How:要计算的和用来计算的东西有什么关系?Why:这个关系应该表现为什么样的数学结构(运算),为什么是这个结构?Meaningful:是不是还有其他的关系或者运算可以用来解决这个问题?这个问题对我有什么意义,能够帮助我更好地理解某个数学概念或者数学方法吗,能够帮助我加深对数学和世界的认识吗?
WHWM用于教和学
实际上,学会问问题,是学习和研究的最重要的能力。如果我们把WHWM这四个问题放到教学内容和方法上来,那就是:
What :学什么,教什么,为了什么要教和学这个?
答:教和学知识生成器,教和学学科大图景。为了创造知识、创造性地运用知识、欣赏知识的创造和知识的创造性使用,为了培养探索世界的人,为了培养更好地理解世界和自己的人而教和学。
How :怎么学,怎么教?
答:通过联系来建构学科概念地图,通过具体知识和研究案例(创造体验式学习)来理解学科大图景,来学会知识生成器。分解和综合,从树木看到森林,从森林看到树木。
Why :为什么学习这个、这样来学习可以达到这个目的?
答:所学习到的知识生成器,尤其是其中的批判性思维、系联性思考、成长型思维,正好就是能够帮助学习者来做创造知识、创造性地使用知识,以及欣赏知识的创造和创造性的使用。整个学习的方式,基于系联性思考的理解型学习,创造体验式学习,也正好可以帮助学习者更好地学习到知识生成器。
Meaningful: 你觉得怎么样(前面的道理讲得通吗),你觉得你的受众(学生,老师,读者)会觉得怎样,对他们来说,有意义吗?
答:我觉得很有道理,我预期我的受众也会懂得甚至喜欢学这些这样学,甚至觉得这个论证过程也有道理。但是,这个方法确实对老师和学生的要求都比较高,无论是对学科知识的理解的深刻程度和高度,还是在学习态度上对理解的不懈追求。因此,我不预期所有读者都会喜欢本书,喜欢这些个说法,尽管我相信将来这样的人会越来越多。也欢迎你来在看了本书(以及将来的配套视频课程)以后问和回答这个Meaningful的问题。你还可以把你的答案发送给我,例如在这里留言,或者给我发邮件wujinshan@gmail.com。
于是,我们看到,这WHWM四个问题会自然导出我们的理解型学习的教和学的方法。这就是WHWM四问的威力,不管是更小的层面的语文阅读和写作、数学题的求解,还是更大的层面的教和学的方法,我们都可以通过问和回答这四个问题来想得更加清楚。