我毕业的高中——兰溪市第一中学,说让我回家做个报告,从自己的学习经验谈一点对学生和年轻老师们有用的东西。这真是个难题。我从来没有讲过自己的学习经历来着,一般更多的报告是关于研究工作和学习教学方法。我顺便把我大概想讲什么在这里整理一下:为了理解世界和自己而学习。说还要介绍一下我自己。那就从介绍自己开始。
先说说我的学习经历。我的小学第一位数学老师自己小学毕业。我上课经常站起来说,“老师,我觉得这样算更好”。老师说,“那你说说”,或者“那你来在黑板上算算”。我的第二位小数数学老师经常让我讲习题课。从小,我就是同学们的助教。很多时候,不得不尝试各种方法来把事情和同学们讲明白。我从小学到高中,基本上有不做作业的自由,代价是数学物理的试卷答案基本上要我们几个人一起出。小学的时候,代价是每天早上要回答为什么没有做,并且在没有理由的时候去靠墙站着一早读课。班主任就是第一位数学老师,从来不算后账,罚过就完事。初中曾经和整个语文小组争论(老师特意在办公室组织的争论哦)“给青年们的一封信”到底是动宾式短语还是偏正式短语,直到深夜,最后老师帮助翻墙才回的宿舍。大学曾经被数学老师和物理老师推荐了好几本对我影响非常深的书来看,主要是上课和课后问的问题太多了(我觉得啊)。还是初中的时候,我的英语老师经常请我吃水果,因为我老是不背书不背单词但是英语成绩还不错,老师希望我配合一下背一下,这样能够有点正面的带头作用。有的时候,我也会尽力配合一下。但是,更经常的时候,我一不注意就不背了。对了,后来我考GRE的时候,也没有专门背过单词。(一定要问我不背课文不背单词,是怎么学会用的,怎么记住的。答案只有一个:多用,直接理解,直接会用)研究生的时候跟一位教量子力学的老师吵过架:我上课说你这个地方讲错了,老师不服,当场辩论,那位老师输了还要找回来场子。国外上课的时候,遇到三位神老师,怎么问都问不倒。于是,吸引了两个专门来听课的同学,告诉我,来听课就是来欣赏我问的问题以及老师对这些问题的回答的。我上课的时候,经常跟学生辩论,允许他们畅所欲言,但是,条件是必须接受我的挑战性的问题。
从小不做作业,不背书,不背单词,只管想明白,只管问问题,只管找到不一样的思路和解法,直到大学开始做大量的作业,以及研究生几乎天天做作业。
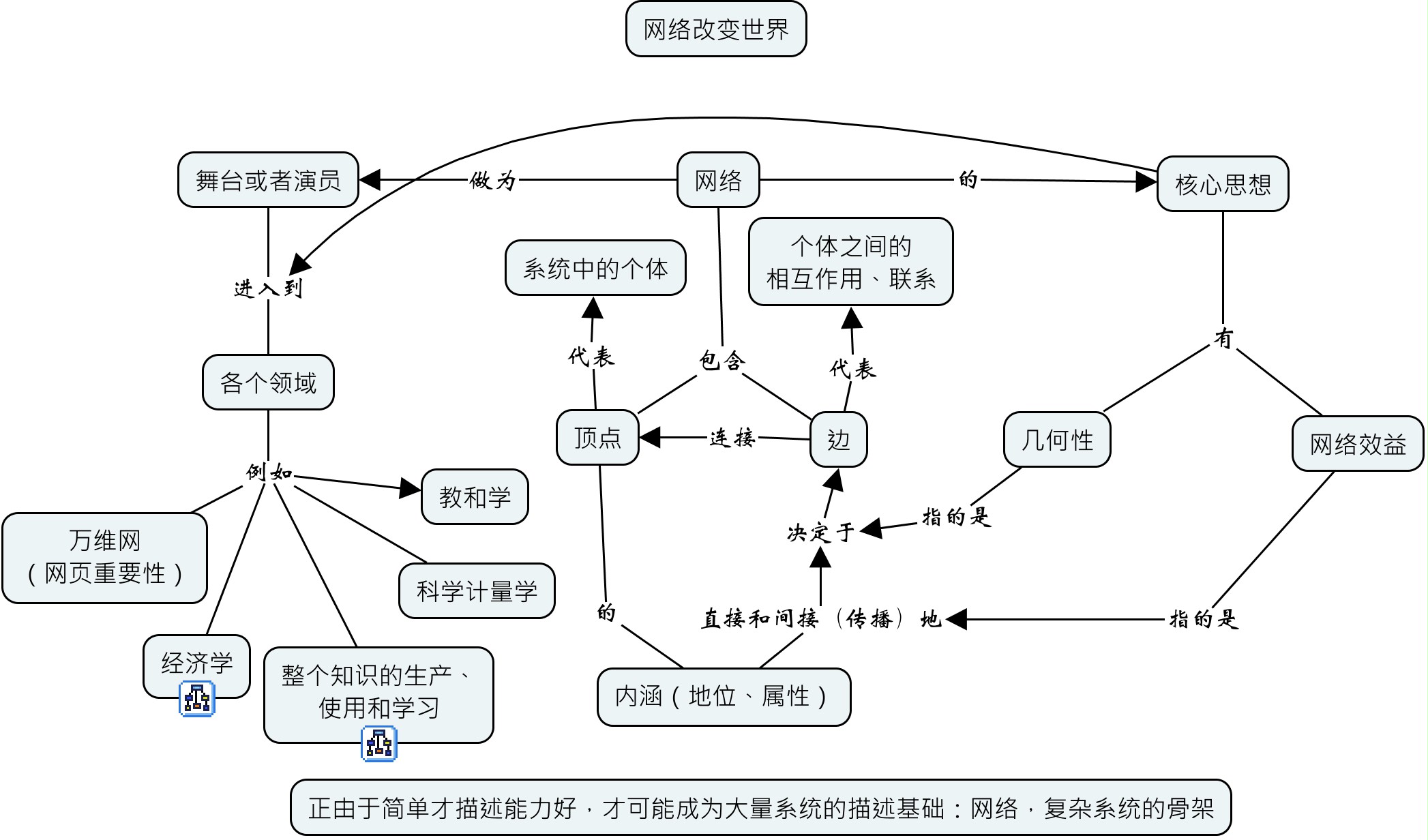
再说说我的研究工作。博士期间挑战了一个统计物理学的基本问题——非平衡定态的定义和计算,尤其是量子系统中的非平衡定态,并且在BBGKY链的基础上,提出了非平衡BBGKY链的求解非平衡定态的技术。对于宏观输运行为,我们不需要求出来非平衡定态,我们有电流的Ohm定律或者热流的Fourier定律可以用。但是,当系统变得更小的时候,量子效益显著,这些定律就不再成立了,甚至导线上的电压降或者温度梯度的图景都不一定正确了,这时候,电流和热流怎么求?没想到这个问题还挺难,做了八年才有点突破。在那之前做过复杂网络。在那里,网络的思想——网络的世界有两样东西:顶点和顶点之间的关系,同时顶点的地位或者说作用,由这个顶点和其他顶点之间的联系来决定,深入了我的思维。同样,物理学的学习和研究使得这样一个相互作用相互联系的视角更加进入我的思维方式:系统的状态由系统里面的个体和个体之间的相互作用决定,甚至时空也是依赖于相互作用的,而不仅仅是物理现象的舞台而已。另一个成了我的思维方式的并且和相互作用的视角相联系的东西是分析和综合:物理学家了解任何问题都喜欢把这个问题分解成更小的结构,然后,看看对某些现象,到底这个系统里面的哪些个部分是关键,甚至一直这样不断地分解下去从而希望了解整个事情的来胧去脉;同时物理学家也希望随时随刻关心把这些细分以后的系统又合起来的问题,看看是不是上一个层次的行为确实可以通过分解到下一个层次以及合起来来解释,或者甚至会发现新的行为。这样的一个分解和综合的思想,被从物理系统推广到社会经济系统甚至更加一般的系统,的时候,成了系统科学的基本思想:还原论和整体论。不过,我向来主张
没有深入到细节,则整体就是假象,觉得好像理解了;没有整体,只有细节,那就是迷途,没有方向
when there is no details, whole is delusional; when there is no whole, all is lost in details without sense of directions.
关于分解与综合,或者说还原和整体,更多的信息可以去看这个帖子”“你好”是“hello”吗,墨水是“ink”吗,“折线统计图”是“折线-统计-图”吗?“或者我的《系统科学导引》书。由于有了这样的相互联系相互作用的视角,有了分解和综合的思想,我做了很多其他领域的研究。我甚至发现,很多时候,只要搞清楚一个领域的大图景(典型对象、典型问题、典型思维方式、典型分析方法、和世界和其他学科的关系),就可以对那个领域的基本问题展开研究,而不需要太多那个领域的基础知识。当然,当真的开展那个领域的研究工作的时候,你需要保证你在这个问题的研究做工作的信息——新问题、新方法、新视角、新结果、新应用,还是新案例。这个时候,你需要去做大量的文献调研,补充基础知识。不过这个时候,是有目标的有方向的补充具体知识,和上课这种泛泛的学习不一样。当然,泛泛的学习的有泛泛的学习的好处,没有具体目标,很多问题可以思考得比较深入比较有系统性。
于是,就做了汉字学习的工作——发现汉字的学习应该运用汉字之间的音形义的联系,汉字本身的音形义之间的联系。极端的例子可以是“木、林、森”、“火、黑、墨”、“木、禾、采、菜、踩”等等。甚至,我们研究了整体层次的问题:按照这些联系,是不是应该先学哪些字,后学哪些字呢,也就是学习顺序的问题;同时由于有了这些联系,在考试的时候,是不是可以通过考察比较少的字,来了解你对其他没有直接考察的字是否认识呢,这样的问题。这就是从整体——有一个汉字之间相互联系以及联系可能可以用于学习的想法,到局部到细节——把每一个汉字和其他汉字之间的联系以及这个字的音形义之间的联系都明确找出来,再从局部——这个联系如何在每一个字的层次上用于学习,到整体——整体的学习顺序和检测顺序的问题。这个例子也很好地体现了相互作用对于问题解决的意义——如果汉字之间没有联系,则这一切都免谈。
类似的,实际上,经济的产业部门、产品之间也存在这样的关系:一个产品成为另一个产品的一部分,正好就像汉字一样。类似的,实际上,科学研究工作之间也存在着这样的关系:一个研究工作成为另一个研究工作的一部分。类似的,实际上,在其他学科的学习中,也有类似的关系:一个数学或者物理的概念成为其他的数学或者物理的概念的一部分。于是,我开始思考,能不能把这样的关系用某种一致的方式来处理呢?能不能在实际教学中用好这样的联系呢?
这两个方面合起来,再加上我在研究工作中对学科大图景的特殊作用的重视,就成了我后来研究比较多的“广义投入产出分析”,以及教学中用的比较多的“理解型学习——以学科大图景为目标的,系联性思考和批判性思维为基础的学习”。
当然,由于来自于物理学的在研究工作中对实验的推崇,我还做一点能够描述实际实现现象的博弈理论的研究。量子力学基础是另一个我做的比较慢但是一直在研究的领域。对于不容易想通的事情,我总是有非常大的兴趣,并且持之以恒。同时,由于这么多年在相变和关联函数上的训练,很多时候,这些也成了我研究其他问题的视角和技术。
从这个总结,我发现,第一,我确实比较反叛,或者说追求一个不一样,不管是在学习、研究还是在教学中;第二,确实一门学科的核心和基础的问题,总是对我有致命的吸引力;第三,我确实很喜欢想明白事情,不断地追问为什么,并且希望跟人分享想明白的事情,以及想明白的方法。当然,这些都不是官方介绍吴金闪的版本。官方版本我一般是这样写的:吴金闪,毕业于University of British Columbia(不列颠哥伦比亚大学),物理学博士,就职于北京师范大学,系统科学学院。研究工作涉及统计物理学、量子力学、科学计量学、博弈论、投入产出分析、汉字以及一般概念的教学。一直在实践和呼吁没有边界的研究和教学。至于如何把前面的学习经历、研究工作、教学以及这个官方版本合起来,那就看主持人的好了。
完成了这个介绍一下自己的学习经历和研究教学工作之后,下面的问题是,我打算讲什么,以及如何把讲的东西和介绍结合起来。
首先,我想告诉大家,要为了理解世界和自己而学习。一中的学生,大部分将来都是需要做引领社会前进的人的。做不了引领者的可能就是一直没找到应该去引领的方面。有的人的人生目标可能是找个好工作。那么,什么是好工作?能够赚很多很多钱,还是能够赚差不多够活着的钱?当然,如果你能够从钱本身获得足够多的乐趣,那么,把好工作或者说人生目标定为钱,也挺好的。如果不是这样,而是你可以从钱带来的社会地位、生活本身等等获得足够多的快乐,那就稍微差一点,但是把钱当成目标也凑活。但是,很多时候,你的快乐可能不直接来自于钱,或者来自于钱带来的地位和生活,比如说,有几个能够交心的相互取暖的朋友,比如说有几个时时挑战你让你痛苦并且快乐的问题,比如说美妙的社会的或者自然的现象。这个时候,有钱,当然,有帮助实现这样的快乐,但不是直接的。这个时候怎么办?我建议你那就去直接追求这些你认为快乐的源泉。例如对于我来说,有值得我不断地去挑战的问题,挑战中的痛苦,以及部分解决时候的快乐,是最大的快乐。忽然之间把某个问题想明白了的快乐是巨大的快乐,尤其是经历想明白之前的痛苦之后。有的时候,甚至看起来解决了带来的短暂的快乐以及之后更大的痛苦,当最后找到真的解决方案的时候,回头看,也是非常大的快乐。再比如,有几个在某个方向上能够交流的一起来思考这些问题的快乐,也是巨大的快乐。再加上我特别喜欢去追寻所谓的事情的本源,这就使我认识到,我应该去追寻物之理。我还喜欢不断地剖析自己,例如,问我怎么会喜欢上物理的,我怎么会喜欢做分解和综合的思考的,人类是如何来处理决策问题对策问题的,等等。因此,对于我来说,更深入地了解这个世界,了解自己,是我的快乐的源泉(之一?)。有的时候,我甚至觉得,反正每一个人都是要从这个世界消失的,一个个体的人所经历的所有的都是短暂的,那么,到底为什么而活着呢?我是觉得如果我的思考使得这个世界变得稍微不一样了变得稍微更美了,或者至少有其他人来受我的思考的启发,一定程度上继承了我的思考了,那么这个活着就是值得的。
不久的将来,所有的重复劳动都会被机器代替,你会有足够多的机会什么也不用做就能有饭吃有地方住。想想,那个时候,你想干什么,才能活得最快乐。你可以找一份工作,周一到周五咬着牙去上班,盼着周末,然后周末去做自己喜欢的,或者更经常不得不带着孩子去做孩子喜欢的,或者你认为孩子会喜欢的,或者你认为“对孩子将来好的”事情。人生很多时候都会是柴米油盐酱醋茶这些事情,你可能还要每天买菜做饭(本来就喜欢做饭的除外)。学习的目的不是给你准备一些技能和知识的基础,将来你还去找一份工作来活着,而是认清楚自己,找到自己的快乐的源泉,或者至少企图找到这个源泉。
这就是我想告诉我的小校友们的第一件事情:学习是为了找到自己,找到自己快乐的源泉,或者至少去寻找这个源泉,而其中重要的一种源泉就是为了更深入地“理解实际和自己”。
我想告诉大家的第二件事情是,我们可以怎么做来找到这个快乐的源泉,尤其是,如果你的源泉也可能和更深入地“理解实际和自己”接近的话。这个做法叫做理解型学习。要把学习和思考当做生活的常态,要把提出和面对新问题当做生活的常态,让每一天都有一个不一样,你或者这个世界不一样了。不要把记忆当做最基本的学习手段,而是要依靠理解。我们不可能为生活中遇到的每一种场景都准备好答案。因此,我们也就不能做信息存储器和搜索引擎:我们知道了每一个问题的答案,当遇到问题的时候,只要在存储器里面找到对应的问题就可以,然后,运用存储这的答案,就可以解决问题。这不是我们学习生活思考的态度。我们要成为能够提出面对和解决新问题的人,让生活的每一天都充满挑战,充满失败,偶尔也成功一两次,充满快乐。我将用一些具体的例子来展示可以怎么做,哪些做法要避免,还有为什么要以及不要那样做。
下面是之前的一些这样的例子的帖子,我会在报告中选择使用。
生活口诀化,学习口诀化,拿什么口诀对付未来呢?
为什么不要直接教孩子1+1=2?
理解型学习一例:逸儿自己学会的乘法除法比大小
理解型学习一例:笔顺、部首还是理据
使用概念地图帮助理解型学习的四个层次
退括号的机械式学习和理解型学习
词汇层次的理解型学习
什么是一个学科的核心概念和大图景?
高中物理基于“大图景”的教学体系
数学四步和数学解题六问
WHWM分析方法
什么是概念地图,以及吴金闪《教的更少,学得更多》
使用概念地图帮助理解型学习的四个层次
我还会做一次实际课堂展示,说明,如何才能用理解型学习做到“教的更少,学的更多”,也就是用更少的知识和例子的学习,来帮学生更好更深刻地体会到学科大图景、来喜欢这个学科、来学会学习方法。我在考虑用量子力学的例子,对比绳子上的波、经典硬币和光过偏振片,来了解:物理学(或者科学)是企图构建一个能够复现实验或者观察结果的心智模型;量子系统的行为要求比较特殊的心智模型,硬币(经典概率)和绳子上的波(Newton力学)这样的经典模型,是不能帮助理解量子系统的行为的;对比的方式,有的时候能够帮助识别出来事物的关键点。
标题:为了理解世界和自己而学习
报告人:吴金闪
摘要:在这个报告中,吴金闪将从自己的学习经历、研究和教学工作出发,跟大家分享“为了理解世界和自己而学习”的快乐,以及实现“为了理解世界和自己而学习”的方法。
照片(提供在这里,万一主持人需要的话,不知道为什么旋转了90度):