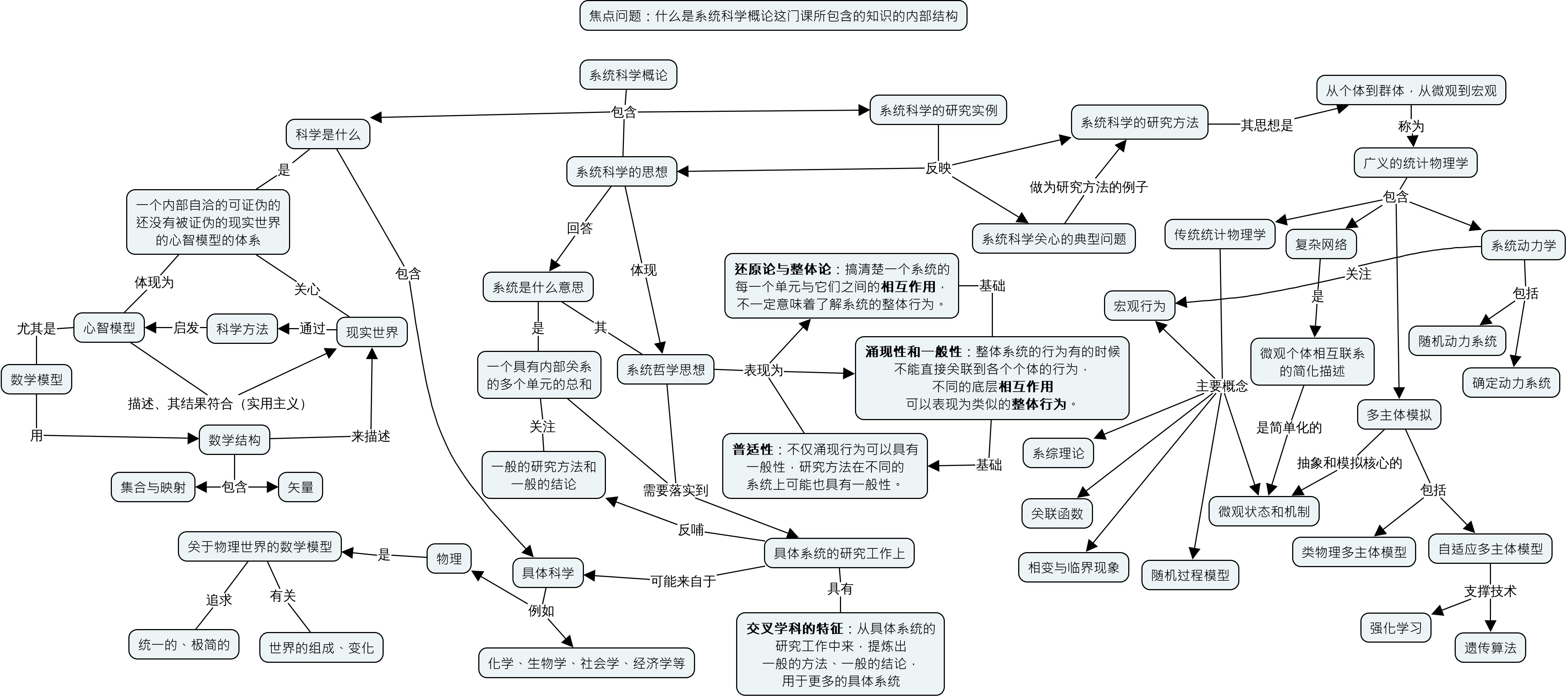
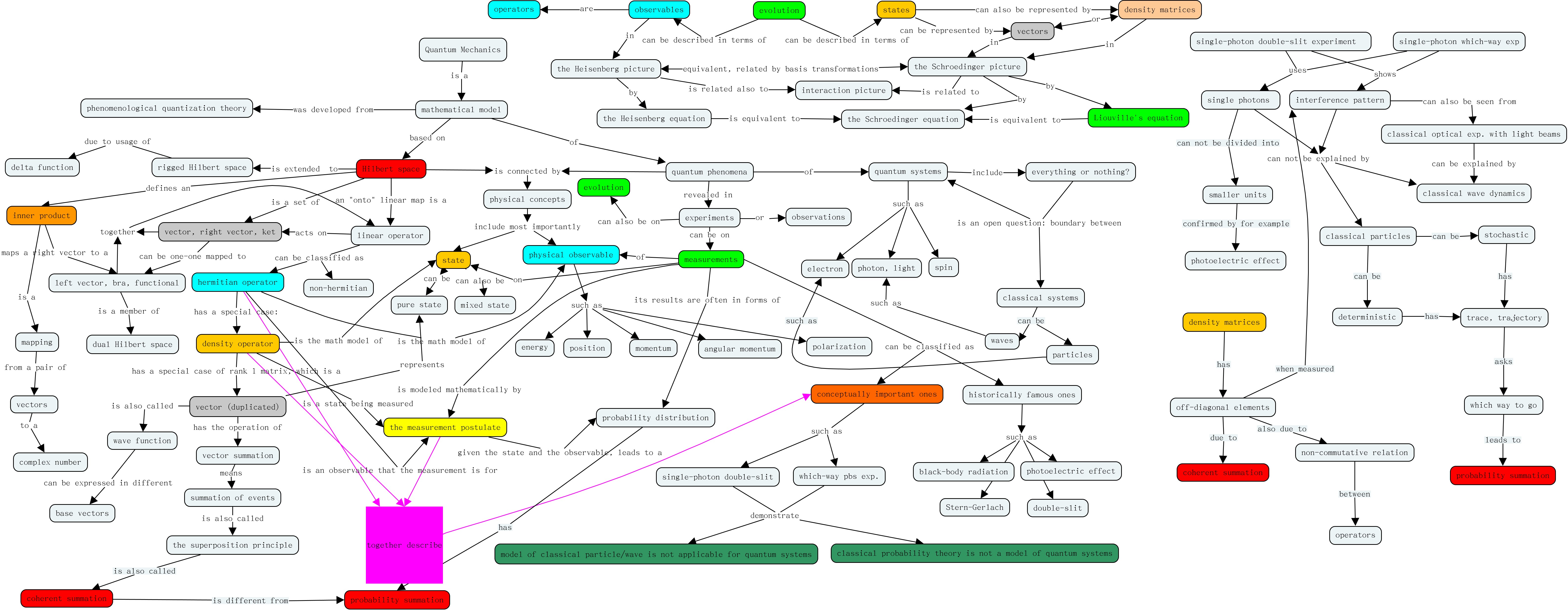
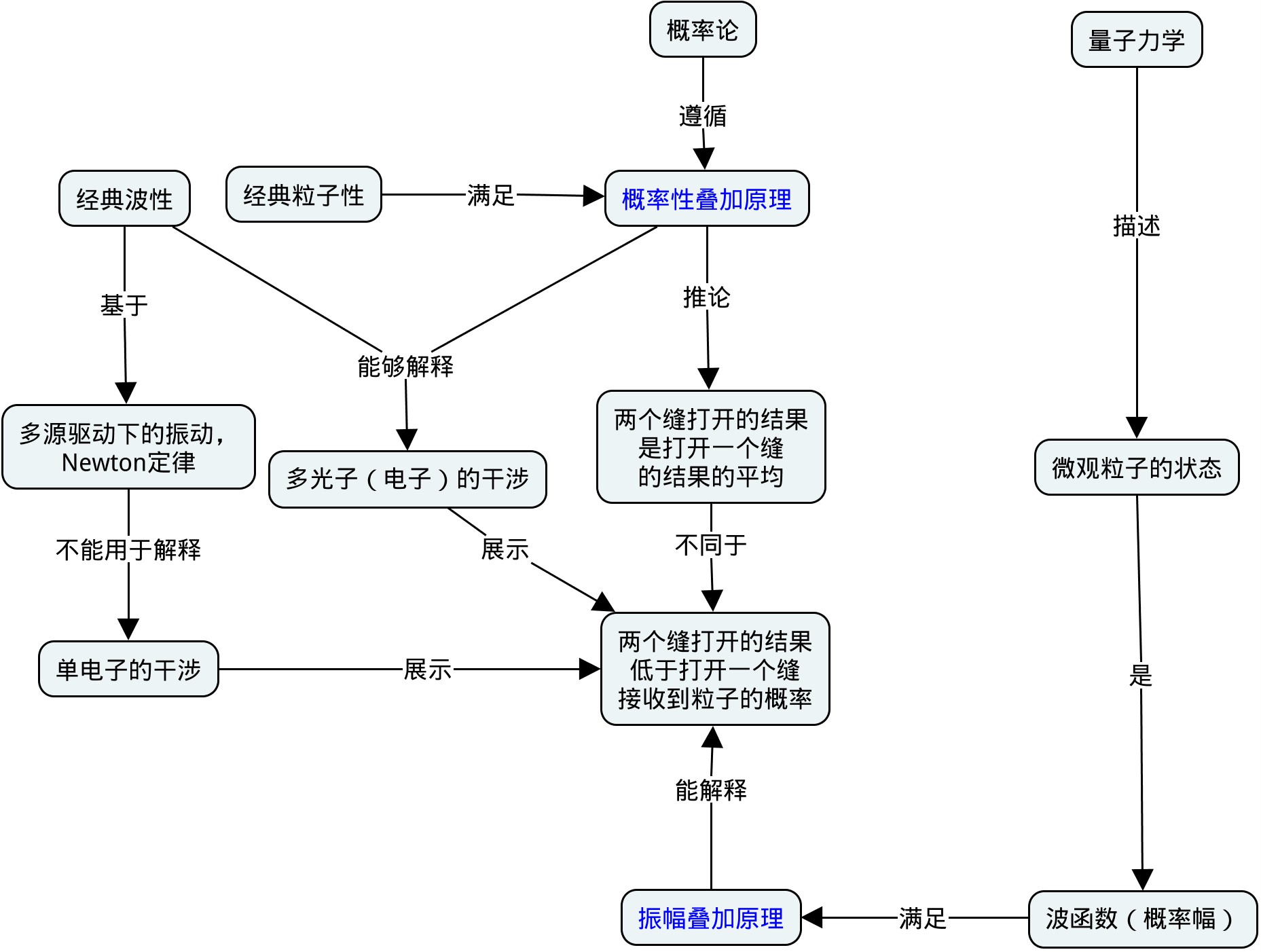
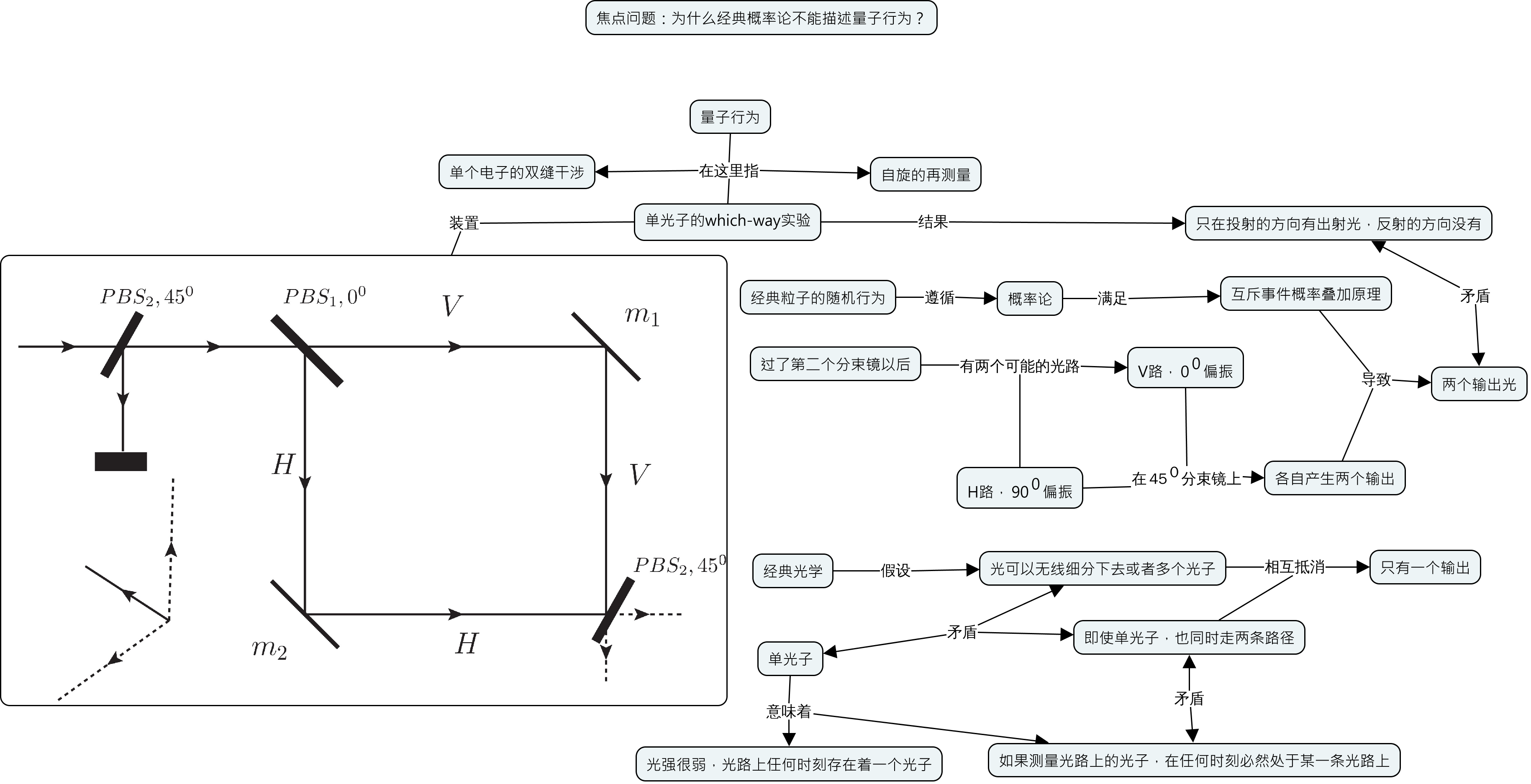
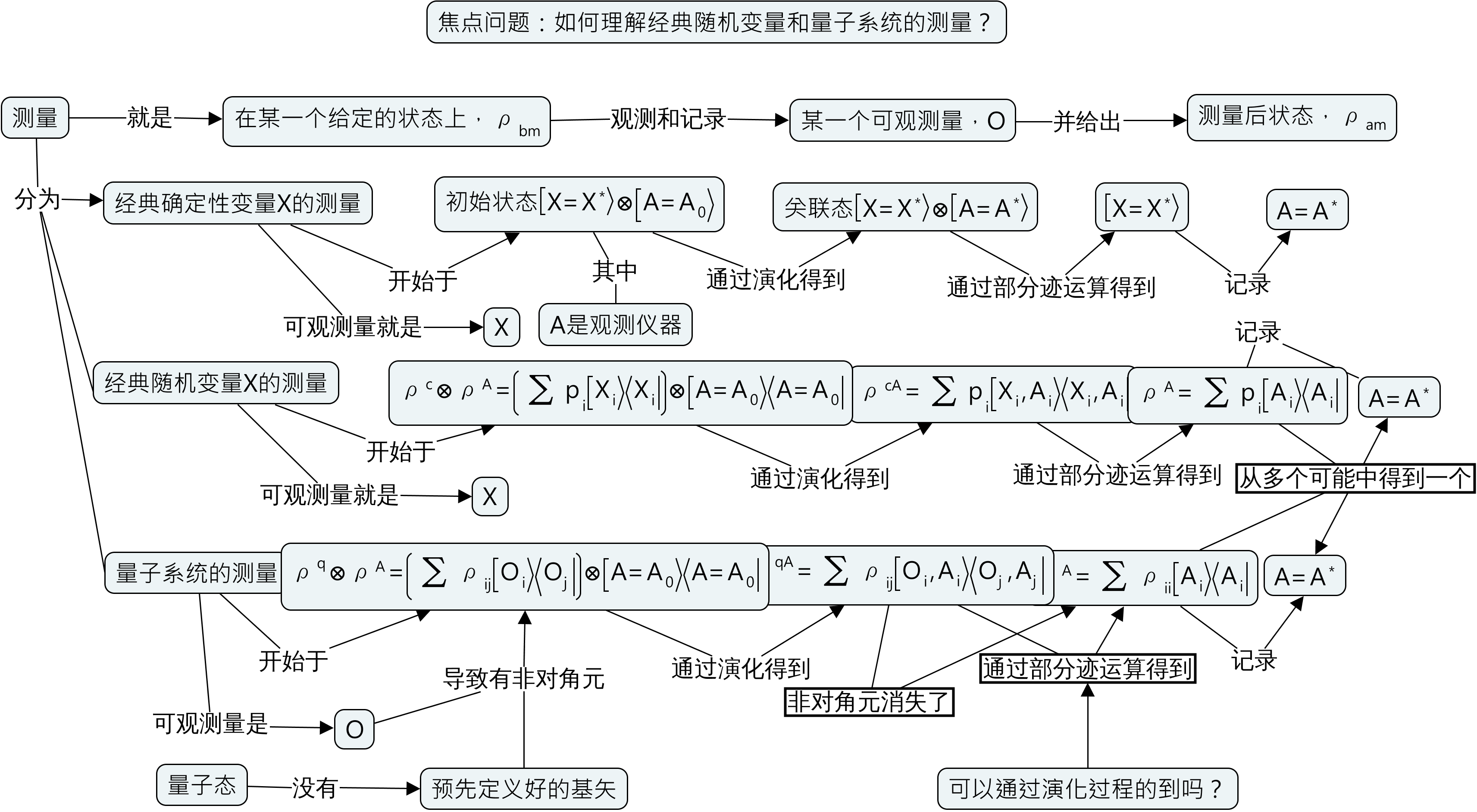
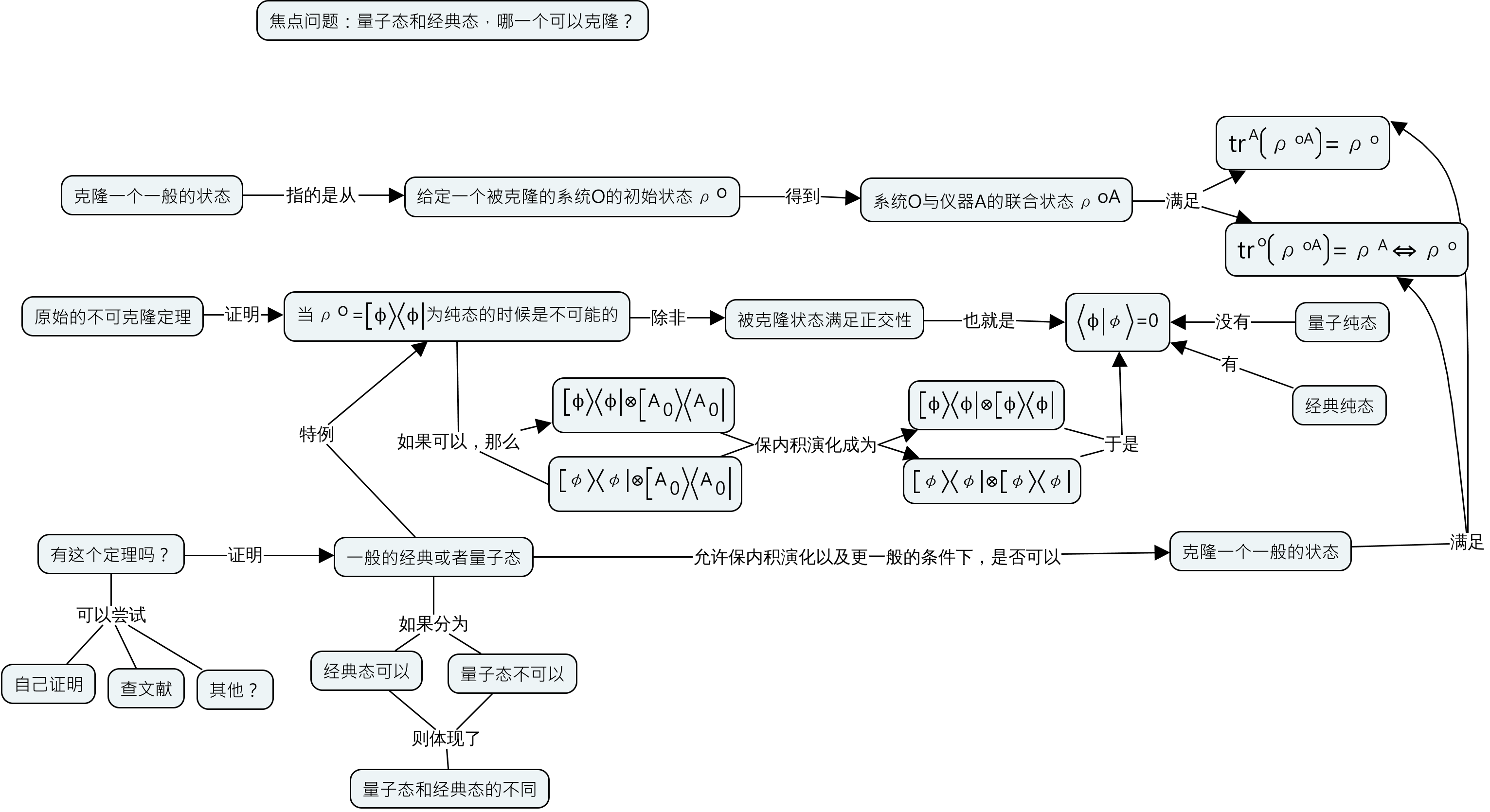
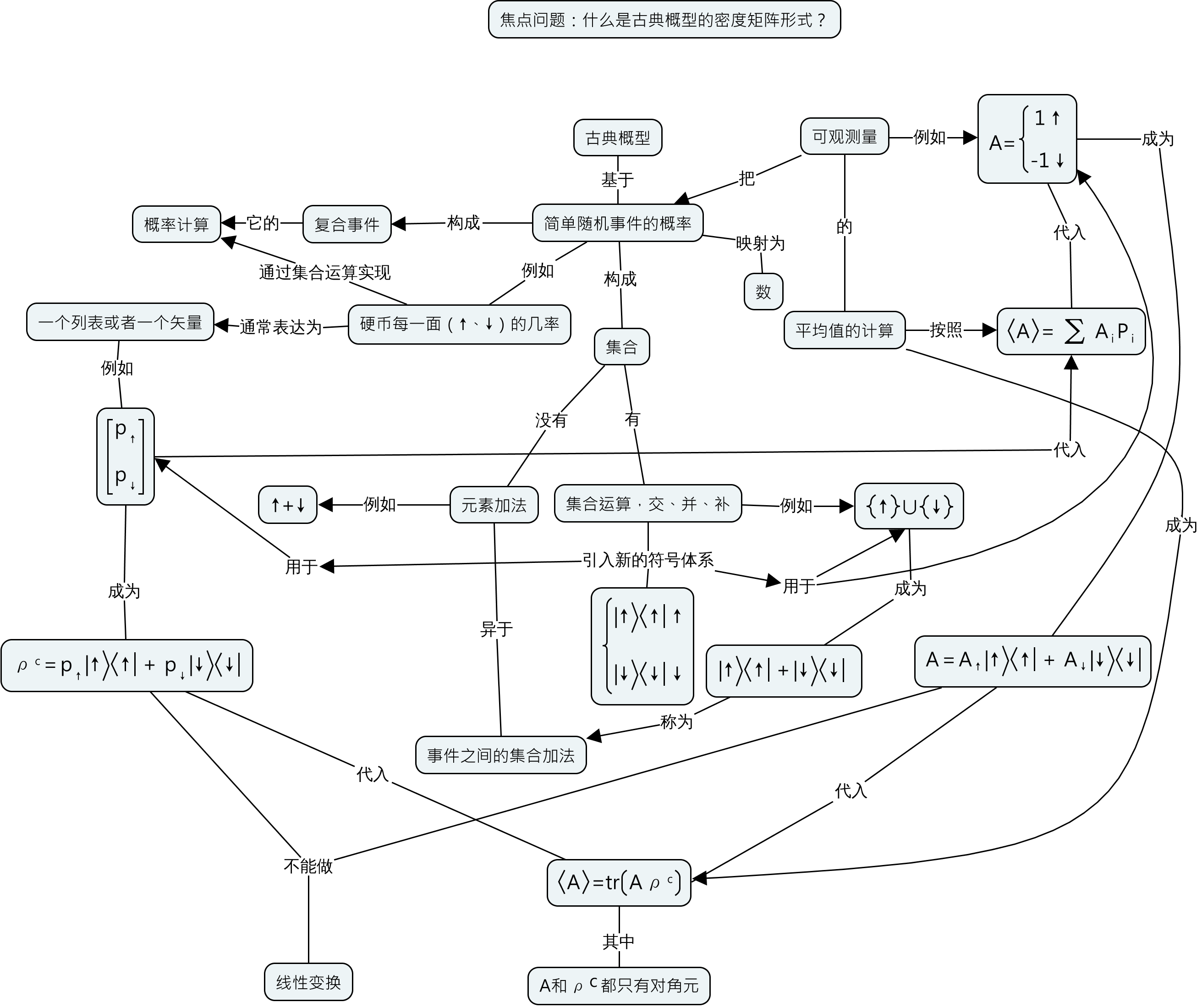
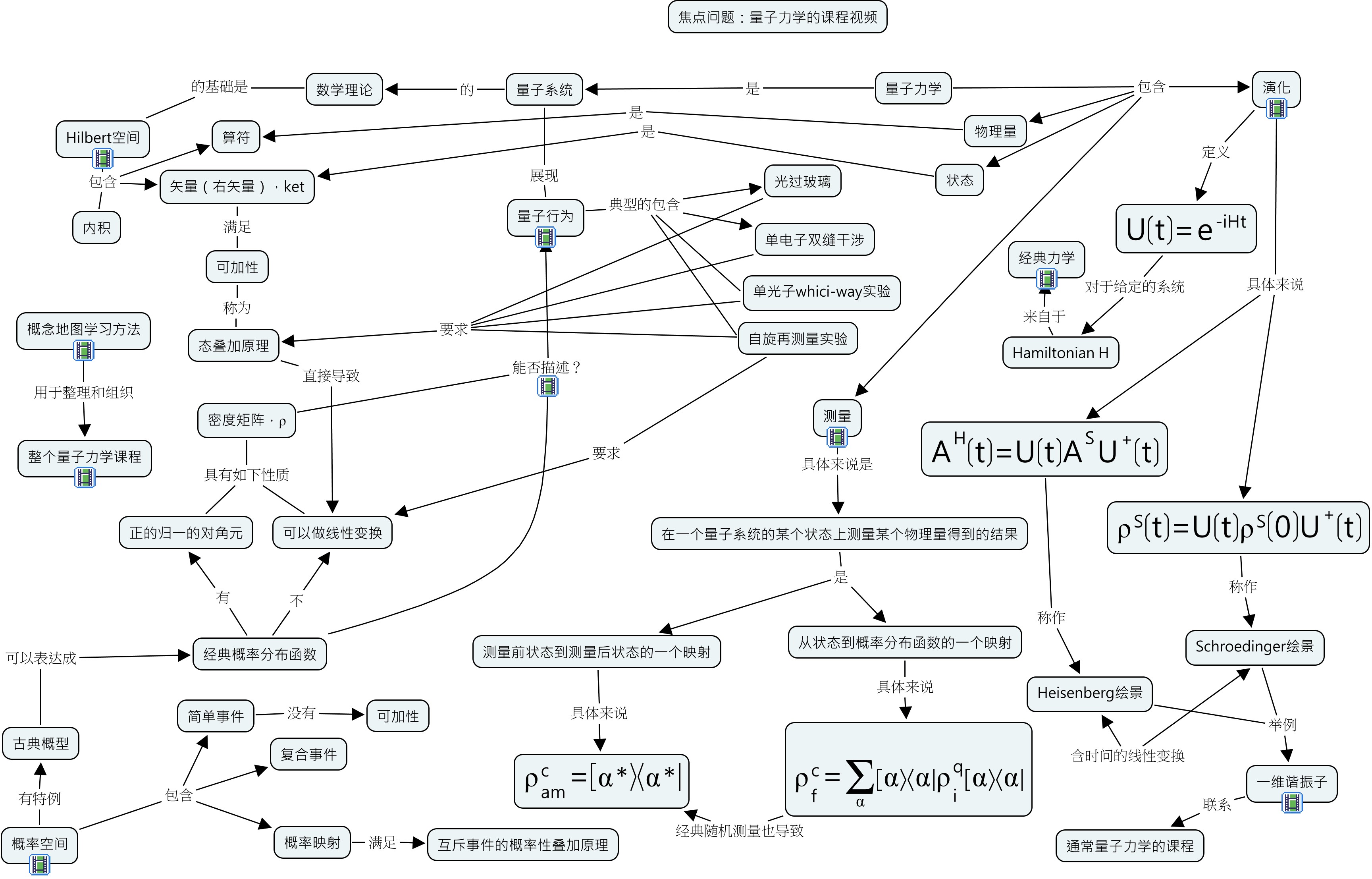
概念地图以及背后的系联性思考、批判性思维是理解型学习的基础,而理解型学习有助于把问题真的搞清楚搞明白并且通过考察事物之间的联系来帮助提出新问题、找到新方法或者发展新应用。按照理解型学习的层次,我把在概念地图的使用分成以下四个层次。
第一、知识高速公路基础架构。把人类知识的主干概念和概念之间的联系找出来,整理成为一个知识结构大框架。注意,这样的框架不是概念的罗列,也不是概念之间关系的罗列,而是一个概念和概念之间的联系构成的有结构的网络。这个网络整体来说,要具有层次结构(大概念到小概念),要有超越层次结构的长程连接,还要有对概念以及概念之间的联系的重要性度量。这个重要性可以内生的来自于这个网络本身,也可以来自于对学科对认识世界等其他方面的考虑。例如,简单粗暴地,可以用概念和关系连词出现的频率来度量重要性。当然,将来的目标是当包含走够大的知识系统之后,这样外生重要性都会成为内生重要性。
第二、课程和课程体系的设计。在这个知识高速公路体系的基础上,或者局部的学科和课程的概念地图的基础上,我们就可以实现针对课程和专业大图景的课程设计。所谓大图景,就是这个专业的典型研究对象、典型思维方式、典型分析方法、典型应用或者其他和世界以及其他学科的联系。大多数时候,具体的知识都会在课程结束以后很短的时间被忘记,但是大图景这样的东西,是进入思维,伴随一辈子的。当然,没有具体知识和具体例子,学生不可能领会到这个大图景。只是,学习的目标不能直接就是那些具体的知识和规则,例如学会怎么算乘法算微分算积分。我们需要围绕着习得学科大图景的目标来选择教什么学什么。
第三,在具体教学、读书(获取信息)、写作(表达信息)的环节,要鼓励深入思考,思考联系,思考为什么,思考WHWM问题。也就是What(主要信息是什么),How(怎么来表达和构建这个主要信息的),Why(为什么这样构建,为什么表达这个信息),Meaningful(对于读者来着,意味着什么)。在思考这些为什么的时候,还需要主要围绕着学科大图景来思考。也就是回答“我为什么选择这个例子来教学或者学习”,“我想通过这个例子来体现什么大图景,为什么能够体现”等等这样的问题。
第四,在作业、诊断和考试阶段,借助概念地图的形式,或者直接通过让学生来制作概念地图,来促进学生的理解型学习。例如,在考试的时候,可以想办法运用概念之间的联系来做到“考的少,考察得多”(让学生通过做更少的题来了解学生的学习状态知识掌握程度)。例如,在诊断的时候,可以通过学生制作的概念地图更加准确地把握学生的在理解上的问题,是某个概念不知道,还是对于这个概念和其他概念之间的关系理解不到位,还是更上层的概念的理解有问题。
关于整体的设想和我们做的事情,可以看我的书《概念地图教学和学习方法》。我们也在北京师范大学《学会学习和思考》课程上做实践上的探索。
第一个阶段的实施,我自己是做不完的。不过已经开始在数学物理等方面实施。另外,联系到Wikipedia已有的知识库,以及Wikipedia的成长本身,这件事情还是有希望的。
第二第三的例子可以看《概念地图教学和学习方法》,以及在这个博客上检索“理解型学习”来看到其他的帖子,例如高中物理基于“大图景”的教学体系。
第四个方面比较细节,还没有仔细整理,但是其中一些标注“理解型学习”的帖子也有例子,例如,鸡兔同笼问题的理解型学习,并讨论方程和构造解法的关系、“四舍五入”的机械式学习和理解型学习、理解型学习用于题海战术、退括号的机械式学习和理解型学习。
其实,我们关于汉字学习和诊断的工作,也可以看做是一个汉字的理解型学习体系。实际上,这个工作是我们真的实际开始做这个概念地图和理解型学习的起点。汉字学习的文章可以在这里找到。这里还有BBC对我们这个工作的评论。还听说在实际教学中发挥了点作用。做的东西能够对其他人有用是好玩的事情。
今年的亚太地区概念地图(中文会议网站,Conference site in English)会议上,我会报告一下这四个层次,结合我们在《学会学习和思考》课程的实践。
多多努力,争取以此改变教学和学习,让孩子们避免背一张又一张的乘法表,开始思考这到底在干什么,开始表达我喜欢吗。