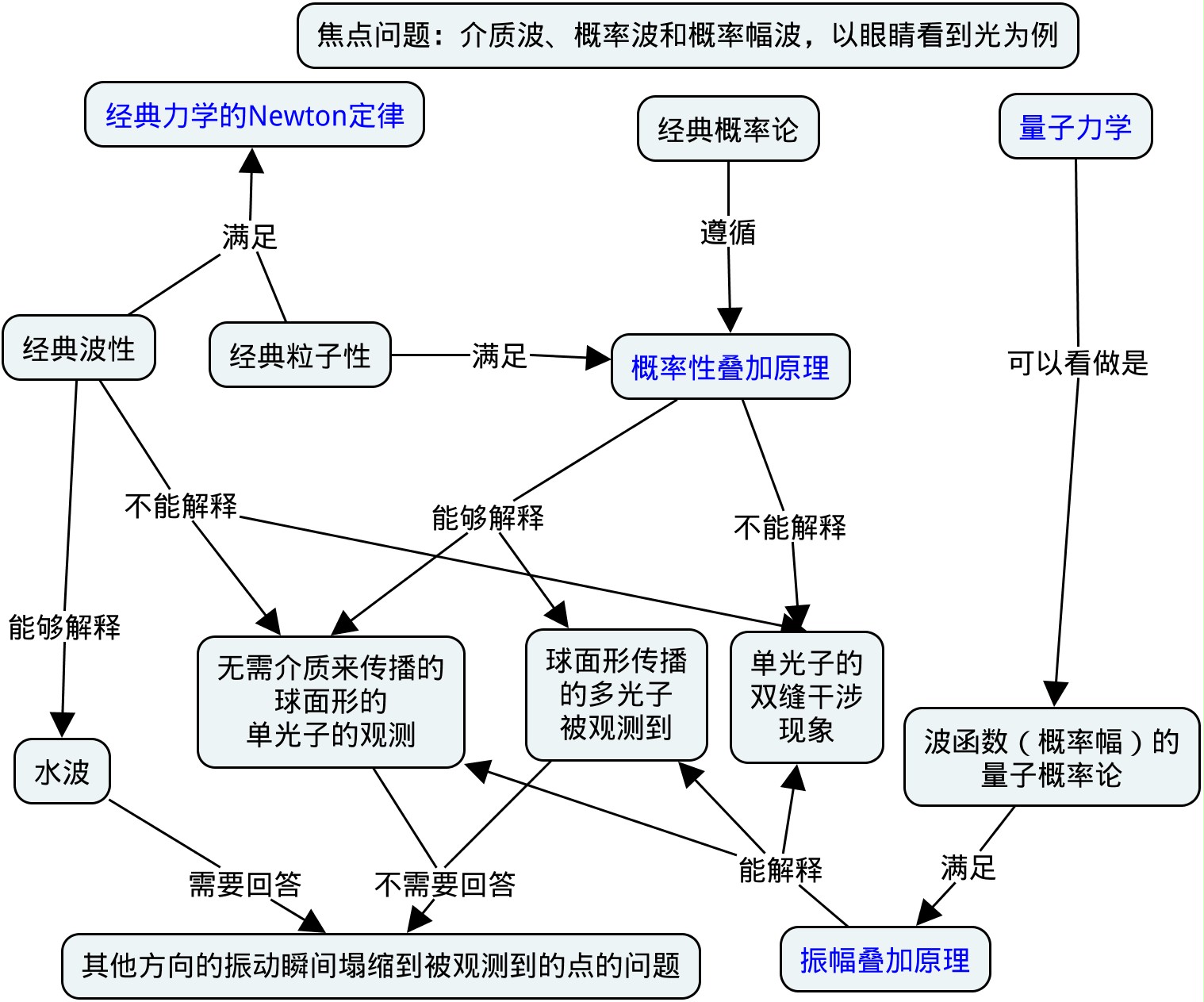
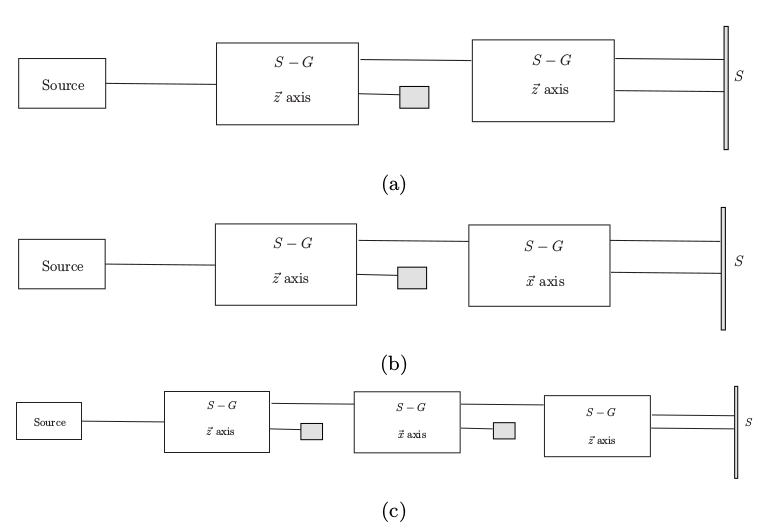
今天上课,讲了无介质波的叠加原理——z方向向上态和z方向向下态可以加起来变成x方向向上态,或者说x偏振和y偏振可以加起来变成某个角度的偏振光,而不是一会儿x一会儿y偏振的组合。忽然想起来,其实,我们能够看到光,这件事情是多么的神奇啊。例如,Einstein就曾经特别想不通这件事情。
白炽灯的光,我们天天见,从来不觉得神奇。连多想一下都不会去想,如何神奇呢?待我慢慢道来,来挑战你的思考。
先看水面的波:扔一个石头(假设石头特别小,看做一个点),水波沿着水面扩散。如果在某个地方有一个观测者——例如一个浮漂,则过一段时间,水波传播到了那个地方,浮漂就会动,也就是观测者看到和水波。这个时候,基本上可以预测,沿着某个圆圈(石头入水处为中心经过这个浮漂的一个圆)的其他地方都可以观测到水波。这个水波很好理解——很好理解可以解释为原则上可以通过牛顿定律来计算。
再来看灯泡发出来的不神奇的光:假设灯丝特别小,看做一个点,则我们会看到和水波一样的事情——当某个地方的观测者看到光的时候,我们可以推测,同样大圆(这时候是大球)的地方的其他观测者也会看到光。当然,由于光的传播速度很快,有可能我们的日常生活体验会告诉我们说,只要一个地方有光任何地方都会有光。
为了解决这个问题,我们需要做两件事情:走的比较远,以及让灯丝每个时间段里面仅仅发出一个光的能量单元,或者一个批次的光的能量单元。这样的一个实验装置是有的,而且这样做好像很无辜啊,没什么特殊之处。现在,我们沿着这个无辜的思路来看看特殊之处。
在这个对于把光看做是水波的第一阶段的认识,我们发现,实际上,我们是把光相当于看做是通过某种介质往外传播的东西。这样,我们就有了一个光和光的传播的心智模型——介质上的振动,和水波类似,只不过沿球面向外传播。这个看起来好像很有道理,也一点都不奇怪。
当然,实际上,我们知道光的传播不需要介质,也不可能有介质。这个需要做个实验来证实,例如第一个让光在真空中传播一下,第二个做一下著名的迈克尔逊-莫雷实验。我们在这里就先承认光的传播不需要介质。这时候,我们再来看,白炽灯的灯光在某处被一只眼睛接收到这件事情。
那先这样看:试试豌豆射手射向四面八方的豆子的模型。灯泡光发出来的光,可以看做是由去往四面八方的一个个光子构成的一群光子合起来的效果。针对这个模型,眼睛能够接收到光也一点都不奇怪,就好像有一个圆形的弹幕,其上任何一点都可能接收到豌豆射手射出来的豌豆。为了看到这样的一个解释的不足,我们来调整一下光源——让光源在任何一个时刻只能射出去一个光的能量单位(称为光子),就好像豌豆射手在任意一个时刻(中间可以特意做成某个时间的间隔)仅仅射出去一个豌豆一样。这样的单光子光源的调整真的是实验上能够做到的。如果要让现象差不多一样,则需要豌豆或者光子的出射方向是某种意义上的随机的方向。
这个时候的随机有两种形式:一种是,任意一个时刻出射的光子都可能向着任意的一个方向,也就是一个所有的方向都具有同样大小的概率密度的概率分布函数;另一种是,任意一个方向上都具有概率密度幅的,整体上表现为所有的这样的概率密度幅加起来的某种分布函数(量子力学的语言,称这样的密度幅的“分布函数”为密度矩阵)。大概来说,相当于
\begin{align}
\rho^{c} = \frac{1}{Z}\int d\Omega \left|\theta, \phi\rangle\langle \theta, \phi\right| \\
\rho^{q} = \frac{1}{Z}\left(\int d\Omega \left|\theta, \phi\right\rangle\right)\left(\int d\Omega \left\langle \theta, \phi\right|\right)
\end{align}
这些公式都是示意公式,仅仅表示前者是概率相加,后者是概率幅相加的意思。现在,我们来看这两种解释哪一种比较有道理,如果我们用它们来理解眼睛看到光的时候的光的状态这件事情。
我们先来看第一种——概率组合。首先,某个方向上的眼睛能够看到光这件事情在这个模型下,很好理解:正好那个随机的光子跑向了那边,于是就刚好被探测到了。这个时候,在这个时间间隔内,其他任何地方都不会探测到光子。注意,在这里,由于经典随机性的存在——例如当我们观测一个随机的硬币发现是正面的时候,就是因为刚好看到了正面,我们不用去担心那反面的几率上哪里去了,怎么会消失了的这件事情——我们不需要担心其他地方的光子跑到哪里去了的问题:那些地方仅仅是有光子到达的可能,而不是真的有光子跑到了那些方向去了,然后由于某个方向上实际探测到光子,这些其他方向的光子又需要从其他方向消失,或者说相当于“塌缩”到正好被观测到的方向的问题。
注意,这个时候,回到水波的模型。如果水波上,我们也看到了类似的现象——一个石头扔进去以后,在某个方向发现了水波,但是其他任何方向没有水波——则,肯定需要问上面那个问题:其他方向的水波难道就真的“塌缩”到了刚好被观测到的方向吗?因此,我们就发现,由于有这个物质波而非介质波的效果——能够控制一个个光子来传播,而不需要介质来产生振动来传播,实际上,介质波的理解是有问题的:真的需要解决瞬间“塌缩”如何发生的问题。所以,初始的用水波来当做光波的心智模型的尝试是不对的。
上面已经提到了,把介质波改成概率波,可以解决这个瞬间“塌缩”的问题。那么,是不是概率波就是对的呢?这个需要做一个叫做双缝干涉或者Which-way实验来证明概率波模型也是错的。如果是概率波,假设我们仅仅取整个空间中的两个方向来做实验——在这两个方向上各自开一个缝,其他的方向上都挡住。先测量仅仅打开一个缝的情况,得到一个经过这个缝到达屏幕的一个实验结果——一个光子达到屏幕的分布函数。这样得到两个分布函数。然后,在考虑概率叠加原理,当一个事情有两种互斥的方式发生的时候,整体的结果等于两个结果的概率相加,于是,我们就得到了打开两个缝的实验结果——应该是分别打开的情况下的概率相加。然而,实验结果发现,不是概率相加,同时具有相长和相消的效果。相消的效果是不能够用概率相加来解释的,如果一定的概率妈妈给孩子五块钱,一定的概率爸爸给孩子十块钱,则平均来看孩子的钱肯定在五块到十块之间。但是,量子的实验告诉我们,有可能得到两块钱,或者二十块钱。这个仅仅在做矢量叠加的时候才有可能,在概率相加的时候是不可能的。
这样,我们就被逼又回到了光子的各个方向概率幅相加的心智模型。可是,这个模型的数学形式和介质上的波很像——在那里,振动方向可以做矢量叠加,于是也就会出现不在五块到十块之间的情况。
问题又来了,如果确实像介质波,那么,我们就又要问,如何来理解瞬间“塌缩”的问题:在某个方向上看到光子之后,整个空间就没有其他光子了,这个看起来,相当于,把观测值钱的其他各个方向上都具有探测到光子的可能性,全部都“塌缩”到了观测到光子的那个方向了。如果确实是这样,将会是大问题:我们可以离光源很远很远,几百万光年,于是,其他方向的光子完全不可能用任何方式传播或者说“塌缩”到观测到光子的方向上去。这怎么办?
其实,这还是用了介质波来理解概率幅波。几率幅波真的没有表示有真的光子传过去的意思,因此,也就不需要在探测到光子的那个时刻,把其他方向上的光子传回来的这个步骤。如果是介质波,就需要这一步。因此,在介质波上也就看不到这样的现象:仅在某个方向上探测的光子,其他方向完全没有探测到光子。
在这个思考中,针对不同情况的实验结果,我们尝试了光的介质波模型、概率波模型、几率幅波模型的介质波理解、几率幅波的几率幅理解。我们发现,只有后者能够解释眼睛看到光这件看起来如此简单的事情。当然,我们还有一个隐藏的要求:不管哪个光子的实验,其结果,都可以用统一的理论来计算和理解。
通过这个例子,在知识上,我希望能够促进对几率幅波的理解,能够促进对什么是科学以及科学和数学的关系的理解——科学就是一个系统化的能够得到和实验现象相符的可计算分析的心智模型的集合;在思维方式上,能够学会不断地层层递进地做批判性思维和对比性系联性思考。同时,我也想通过这个例子说明:学习就是学会一双眼睛,从平凡中看到神奇,从神奇中复又看到平凡或者平凡和神奇的共存。学习是为了理解世界。