吴金闪的工作和思考

有人问，单光子光源怎么做的，纠缠是怎么回事？好吧，我就顺便说说这个。

数学和物理的准备

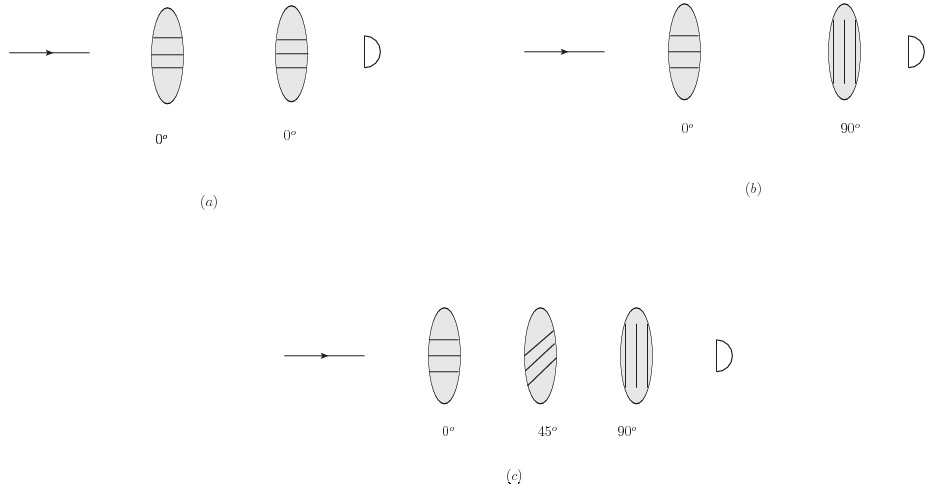
不过，这也是一个需要挑战智力的问题，并且需要一点点量子力学和经典概率论的基础：第一、量子力学对于量子系统的状态的数学描述是波函数或者说密度矩阵，其背后是状态本身是具有可叠加性的矢量，并且由于这个矢量性，我们可以用任何一组正交归一基矢来展开量子态，也就是（其中三个方向分别表示\(45^{0}\)偏振、水平偏振和竖直偏振。如果对于偏振现象还不是特别了解，则可以参看“光过三个偏振片和男人女人过三道门的对比”）
\begin{align}
\left|\psi\right\rangle = \left|45^{0}\right\rangle = \frac{\sqrt{2}}{2}\left(\left|H\right\rangle + \left|V\right\rangle\right), \\
\rho^{q} = \left|45^{0}\right\rangle\left\langle 45^{0}\right| = \frac{1}{2}\left(\left|H\right\rangle\left\langle H\right| + \left|H\right\rangle\left\langle V\right| + \left|V\right\rangle\left\langle H\right| + \left|V\right\rangle\left\langle V\right|\right). （1）
\end{align}
这两行等价。
第二、量子测量可以看作是代表测量仪器的矢量或者说算符和代表状态的矢量或者密度矩阵的内积，也就是
\begin{align}
P_{\alpha} = \left| \left\langle \alpha \right. \left|\psi\right\rangle \right|^{2} = \left\langle \alpha \right| \rho \left| \alpha \right\rangle, \\
\rho^{c} = \sum_{\alpha} \left| \alpha \right\rangle\left\langle \alpha \right| \rho \left| \alpha \right\rangle\left\langle \alpha \right|, （2）
\end{align}
这两行（实际上三个等式）等价。其中的\(\alpha\)代表测量仪器的方向以及相应的矢量。注意，如果确实观测到了某个状态\(\left| \alpha^{*} \right\rangle\left\langle \alpha^{*} \right|\)（也就是所有概率中的\(P_{\alpha^{*}}\)得到了抽样实现），则系统在测量完成时刻的状态是\(\left| \alpha^{*} \right\rangle\left\langle \alpha^{*} \right|\)。这个被称为测量后状态公理。
第三，经典随机对象的描述是
\begin{align}
\rho^{c} = \left(p_{H}\left|H\right\rangle\left\langle H\right| + p_{V}\left|V\right\rangle\left\langle V\right|\right). （3）
\end{align}

顺便补充一下，对于独立随机变量，
\begin{align}
\rho_{12}^{c} = \rho_{1}^{c}\rho_{2}^{c}, （4）
\end{align}
否则称为经典关联随机变量。例如两个完全一致的硬币可以写做，
\begin{align}
\rho_{12}^{c} = \frac{1}{2}\left(\left|HH\right\rangle\left\langle HH\right| + \left|VV\right\rangle\left\langle VV\right|\right) \\
\neq \rho_{1}^{c}\rho_{2}^{c} = \frac{1}{4}\left(\left|H\right\rangle\left\langle H\right| + \left|V\right\rangle\left\langle V\right|\right)\left(\left|H\right\rangle\left\langle H\right| + \left|V\right\rangle\left\langle V\right|\right). （5）
\end{align}

后面，我们会用到矢量的内积——两个正交归一的基矢量的内积满足\(\left\langle \mu \right.\left| \nu\right\rangle=\delta_{\mu\nu}\)，也就是如果是同一个基矢量则内积等于1，否则等于0。

如果你知道这些公式的含义最好。不知道的话，需要达到下面的理解程度，为什么这样可以参考“能看到光是多么神奇的事情啊”、“光过玻璃是一件多么神奇的事情啊”和“光过三个偏振片和男人女人过三道门的对比”：

1. 经典的硬币可以处于概率组合态，也就是要么向上（H），要么向下（V），以一定的概率，这样的状态，这个状态的数学语言就是第三个公式里面的样子。
2. 量子的偏振可以处于概率幅叠加态，也就是代表水平（H）和竖直（V）的矢量直接加起来，以一定的概率幅，这样的状态，这个状态的数学语言就是第一个公式里面的样子。其中两个H和V状态前面的系数决定了偏振的方向。例如\(45^{0}\)的时候，系数都是\(\frac{\sqrt{2}}{2}\)。我们有方法按照方向计算出来这些系数。不过我们不用管具体怎么算。
3. 量子的偏振测量仪器对应着某个特定的方向，例如我想拿着\(45^{0}\)或者\(135^{0}\)偏振的镜片来做测量，这样的状态，就会对应着相应的矢量\(\left| \alpha \right\rangle\)，具体方向和矢量之间如何对应暂时也可以不管（如果仪器在\(45^{0}\)则\(\left| \alpha \right\rangle = \frac{\sqrt{2}}{2}\left(\left|H\right\rangle + \left|V\right\rangle\right)\)，在\(0^{0}\)则\(\left| \alpha \right\rangle = \left|H\right\rangle\)，如此这般），一旦有了这个仪器对应的矢量之后，测量结果是一个概率分布函数（的某一个抽样），这个分布函数的数学操作就是第二个公式里面的样子。

如果以上这些由于数学符号你还是不明白或者被吓住了，那么，下面的理解也算过得去：

1. 经典的硬币的状态是概率组合态。
2. 量子的偏振的状态是矢量叠加。
3. 量子的偏振测量的仪器可以选择某个特定的方向，然后结果依赖于这个方向和量子系统的状态。
4. 以上都是可计算的，仅仅怎么算暂时不管而已。

纠缠的实验实现

现在我们来回答纠缠是怎么实现的，下一节，再来看纠缠会有什么特殊性质。在那之前，我们先来做一个理想实验——真实不好做的但是在脑子里面比较容易做的“实验”。我们假设有经典真随机的硬币。我们想通过这样的经典真随机的硬币来制备一对经典关联的硬币。经典关联状态我们已经在第四个公式中提过。怎么实现呢？我们需要做一个信号分割器，例如网线分割器这样的东西，就是一个信号一分二的接头：一个随机变量进来，两个随机变量出去，并且两个变量的值完全一样。这个信号分割器或者说信号复制器，在经典信号上是完全可以实现的。这样，不管进来的信号是上（H）还是下（V），我们总会得到两个完全一直的随机信号，合起来，也就是我们需要的经典关联随机状态。就好像是一对同卵双胞胎，尽管我们可以不知道其性别，但是我们知道肯定同性。于是，观测一个的性别就知道了另一个。

我们再来看量子的双胞胎怎么制备。有一种晶体可以用来产生一对叫做“下转换光子”的光子对。根据能量守恒和动量守恒的约束，这两个光子的能量和动量是相互确定的，总和必须等于入射光子的能量和动量。其中一个的动量知道了就可以推算出来另一个动量。为了简单计，让我们假设这样的动量的取值只有一种\(p\)，同时对应着的另一个光子的动量取值就是\(P-p\)。\(P\)是总动量。但是，由于我们不知道哪一个光子会取\(p\)，所以对应着两种情形，

\begin{align}
\rho_{12}^{q} = \frac{1}{2}\left(\left|p，\left(P-p\right)\right\rangle + \left|\left(P-p\right),p\right\rangle\right)\left(\left\langle p，\left(P-p\right)\right| + \left\langle\left(P-p\right),p\right|\right). （6）
\end{align}
甚至，这两个光子的偏振也是配对的，这里我们取那个偏振方向总是相同的情形来讨论，
\begin{align}
\rho_{12}^{q} = \frac{1}{2}\left(\left|HH\right\rangle + \left|VV\right\rangle\right)\left(\left\langle HH\right| + \left\langle VV\right|\right). （7）
\end{align}
这里我们用了量子力学的矢量叠加性——如果一件事情有两种发生的可能，并且不能区分到底是哪一种，则状态是这两种可能的状态的矢量叠加。这个矢量叠加性导致了公式（7）和公式（5）的结果不一样。

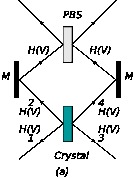
有了双光子的纠缠之后，还可以通过测量来实现更多的光子的纠缠，见例如潘建伟等人的多光子纠缠的工作。具体如何实现就不讨论了，我只截取了其中的一张图，根本上就是设置实验仪器允许某一类的仍然具有多种的情况可能发生，然后，由于这些情况不可区分，系统的状态是这些状态的矢量叠加。因此，就是矢量叠加性的各种巧妙运用。

纠缠的神奇之处和神奇之处的来源

有了数学物理基础，也有了制备的方式，我们来看这个状态有什么神奇的地方。我们通过对比经典关联态和量子纠缠态来看这个神奇之处。

首先，考虑公式（5）的经典关联态。注意，这个时候硬币只能观测到要么向上（H），要么向下（V）两种情况。不过，就关联起来的情况，如果第一个硬币是正面则第二个也是，反面的情况也一样。
\begin{align}
P_{HH} = \frac{1}{2}, P_{VV} = \frac{1}{2}, P_{HV} = 0, P_{VH} = 0. （8）
\end{align}你觉得这个经典关联态神奇吗？我不觉得。

其次，我们来考虑公式（7）的量子纠缠态。我们先来观测一下水平还是竖直偏振，也就是我们在两个光子上都做矢量投影\(\left|H\right\rangle, \left|V\right\rangle\)的测量。于是，按照我们测量的计算方式公式（2），我们得到，
\begin{align}
P_{HH} = \frac{1}{2}, P_{VV} = \frac{1}{2}, P_{HV} = 0, P_{VH} = 0. （9）
\end{align}
这个看起来和公式（8）一模一样，所以我也不觉得奇怪。

奇怪的事情来了：让我们在\(45^{0}\)方向来测量一下两个光子，也就是把公式（1）中的\(\left|45^{0}\right\rangle\)当做\(\alpha\)放到公式（2）里面，其中的\(\rho\)呢分别用公式（5）和公式（7）看看结果是不是一样。这个计算过程我就不展示了，其实也就是把上面的各项套进去以后用好内积的计算规则，就行。暂时就只有相信我了。我们会得到，对于经典的情形
\begin{align}
P_{45^{0},45^{0}} = \frac{1}{4}, P_{135^{0},135^{0}} = \frac{1}{4}, P_{45^{0},135^{0}} = \frac{1}{4}, P_{135^{0},45^{0}} = \frac{1}{4}. （10）
\end{align}
而对于量子的情形
\begin{align}
P_{45^{0},45^{0}} = \frac{1}{2}, P_{135^{0},135^{0}} = \frac{1}{2}, P_{45^{0},135^{0}} = 0, P_{135^{0},45^{0}} = 0. （11）
\end{align}
后者的结果才是和实验相符的。这个结果说明：第一，这样的量子纠缠态具有一个神奇的性质，在任何一个方向的配对测量，都可以观测到纠缠；第二，如果形式上允许经典来测量\(45^{0}\)等方向，则经典概率叠加态给出来的结果和实验不相符。或者说，仅仅在原始的方向，这里也就是水平和竖直，经典测量给出来的关联性的理论结果和实验结果——两者一样，是和量子情形一样的。一旦允许改变方向，则第一经典原则上没法来测这个改变的方向，第二给出来的理论结果也是错的。

因此，量子纠缠的神奇之处在什么地方呢？在于任何一对正交方向上对两个光子的偏振的测量，都给出来完全相关的信息，而不仅仅是水平和竖直这一对方向。然而，经典相关态仅仅在原来设定的方向上完全相关，不能由实验者改变方向。因此，神奇之处不在于完全相关，而在于任何一对正交方向（量子）和仅仅原始的方向（经典）的对比。其实，量子甚至可以告诉你，计算两个光子的测量方向不一样，仍然可以得到一个关联系数，并且这个关联系数能和实验相符。只要用给定方向下的合适的\(\left|\alpha\right\rangle\)代入公式（2）就可以算出来这个结果。也就是说，这个神奇之处，就来自于公式（1）和公式（2）。前者是状态的矢量叠加性，后者是如何从状态来计算给定测量仪器以后得到的测量结果。换句话说，其实，根本上就是公式（1）——态的矢量叠加性，因为公式（2）其实经典和量子的时候都对。

为了保证这个关联性，看起来就好像是对一个光子的测量改变了另一个光子的状态，不管它们离得多远。可是这件事情奇怪吗？经典随机关联变量不是也一样的吗？测量了一个之后，就知道了另一个，也就是说，另一个的状态就已经被改变了。这个关联性本身不是神奇的事情，而是任何一对方向上的测量都具有类似的关联性才是奇怪的地方，而这个关联来自于状态的矢量叠加性。

咱们来做两个这样的计算，首先，如果测量得到第一个光子是\(\left|H\right\rangle\)看看第二个光子是什么状态。我们就用测量后状态公理得到
\begin{align}
\rho_{2} = \left\langle H\right| \frac{1}{2}\left(\left|HH\right\rangle + \left|VV\right\rangle\right)\left(\left\langle HH\right| + \left\langle VV\right|\right)\left|H\right\rangle \propto \left|H\right\rangle\left\langle H\right|.
\end{align}
其次，我们来看，如果测量得到第一个光子是\(\left|45^{0}\right\rangle=\frac{\sqrt{2}}{2}\left(\left|H\right\rangle + \left|V\right\rangle\right)\)看看第二个光子是什么状态
\begin{align}
\rho_{2} = \frac{1}{4}\left(\left\langle H\right| + \left\langle V\right|\right) \left(\left|HH\right\rangle + \left|VV\right\rangle\right)\left(\left\langle HH\right| + \left\langle VV\right|\right)\left(\left|H\right\rangle + \left|V\right\rangle\right) \\
\propto \frac{1}{2}\left(\left|H\right\rangle + \left|V\right\rangle\right)\left(\left\langle H\right| + \left\langle V\right|\right).
\end{align}
更进一步，非常容易验证，如果纠缠态的数学表达式中间缺几项，变成经典关联态那样，则第二个计算得到的结果不一样，
\begin{align}
\rho^{c}_{2} = \frac{1}{4}\left(\left\langle H\right| + \left\langle V\right|\right) \left(\left|HH\right\rangle \left\langle HH\right| + \left|VV\right\rangle\left\langle VV\right|\right) \left(\left|H\right\rangle + \left|V\right\rangle\right) \\
\propto \frac{1}{2}\left(\left|H\right\rangle\left\langle H\right| + \left|V\right\rangle\left\langle V\right|\right).
\end{align}
这个第二个光子状态和第一个观测到的不一样。从这个计算我们看到，我们不需要做时间演化，也不需要做信息传递，第二个光子自然就会随着第一个光子测量结果的改变而改变。这件事情甚至在经典关联态上都是如此。因此，纠缠态并不意味着超距作用，尽管实际上两个光子可以距离很远，因为它们之间根本没有作用，只有超距！完全就是逻辑推导的结果。

类似的问题在测量的时候也会遇到——测量实际上就是一个先建立纠缠再抽样观测到其中某一个状态的过程。那个时候，你可能也会觉得，甚至在纠缠建立起来之后，好像某个信息或者某个时间过程，从你测量的仪器甚至你的脑袋，跑到了被测量状态上。这完全就是假像。我们已经看到只要先建立起来纠缠，这个相关的实现不需要任何时间过程，不需要任何信号的传递，甚至根本就没有相互作用。

神奇的纠缠可以用在什么地方

由于在任何一对方向（不仅仅正交）上的测量都具有这个相关性（正交的话就正好就是完全相关），这样的神奇性质可以用来做很多很多事情。例如量子远程传输、量子博弈、快速因子分解、量子密码等等。具体例子，暂时就不进一步讨论了。

纠缠还可以用来做单光子光源，每次从出来的一对里面，挡住一个，就行了。这样的设备能够很好地保证单光子性。

小结

如果上面的数学公式把你吓住了，或者妨碍了你的理解，这是我的小结：量子态和经典态的核心区别是前者有矢量叠加性后者有概率叠加性；这个区别有数学公式可以表达，可以用来做后续的测量结果和测量后状态的计算；量子纠缠态只不过是这样的一组叠加态它对于任何一对测量都能够给出相关性，有的时候甚至是完全相关，就好像经典关联态一样，但是量子的情形能够对任意一对测量给出来相关性，而经典只能是预设好的方向；这样的相关性就好像是意味着对一个粒子的测量会改变另一个粒子的状态一样，但是我们的计算没有用到时间过程，没有信号需要传播，仅仅是逻辑上的推理，因此不需要真的两个粒子之间有相互作用；类似的事情在测量的时候会发生，那个时候——在纠缠建立起来之后，同样不需要在仪器（或者你的大脑）和被测量粒子之间建立起来什么相互作用。