我很少关心孩子做加减乘除计算的问题,因为:第一,大部分时候算出来的答案是对的;第二,这个问题也实在太低级,有更多关于什么是数学,教什么怎么教才能体现什么是数学,什么是数学的大图景(典型对象、典型问题、典型思维方式、典型分析方法、和世界以及其他学科的关系)这样的更重要的问题需要思考。我真的更加愿意来回答如何才能让学生学会用数学的眼光看世界(发现和提出问题、把问题数学化形式化、求解问题、解的应用和检验以及推广和系统化,这四个步骤中的1、2、4这几步,甚至由于这个1、2、4导致新的数学概念的提出),更愿意去看看数学有哪些典型思维方式——例如不变量的思想,然后问用什么样的例子来体现这些典型思维方式,这样的问题。
但是,今天我发现不是这么回事,在孩子的四则运算过程中存在大量的分类体系和各自问题的特定的方法(顺便,听说高中物理题也成了这个德行:总结出所谓的各种题型,然后对每一种题型有相应的方法。这个太恶心了!)。这个太恐怖了,太让我吃惊了。我一直觉的,根本就没有题型,只有一个一般的方法:那就是思考问题里面有哪些东西,这些东西之间什么关系,这个关系导致了什么样的计算,然后算出来就行了。于是,我尽量克制自己的恶心来做一下这个实在太低级的总结。下面,我们仅仅考虑十进制表示的数字,包含小数点,先不考虑循环小数(其实,以下的总结仍然适用于循环小数)。
加法的计算规则:首先对齐小数点(并且由于小数点对齐了,则实际上各个数位上的数都对齐了;都是整数的话,对其小数点相当于对齐了个位数。但是,总而言之,一句话的概括,就是对齐小数点),然后各个数位,从最右边的开始,做相应数字的(看做一个个的个位数)加法,如果出现加起来超过10的情况,则需要进位,进位需要算到左一位的数字里面,再继续做左一位的加法。
减法的计算规则:首先对齐小数点(并且由于小数点对齐了,则实际上各个数位上的数都对齐了;都是整数的话,对其小数点相当于对齐了个位数。但是,总而言之,一句话的概括,就是对齐小数点),然后各个数位,从最右边的开始,做相应数字的(看做一个个的个位数)减法,如果出现不够减的情况,则需要从左边一位借一个10过来,和当前位上的数字合起来构成“十几”再来完成减法,借位需要算到左一位的数字里面(相当于被减数被事先就减去了1),再继续做左一位的减法。
乘法的计算规则:首先把所有的计算转化成整数的计算,这个时候如果有小数相当于把那个小数做了一次乘以10、100、1000或者更多个10,这些10将来都是要除回来的,记住将来要除多少个。接着就是运用整数乘法。这个时候,要把最后一位对齐(如果非得要这么看,也可以看做小数点对齐,但是,是变成了整数以后的小数点,也就是个位数对齐),接着拿着乘数的个位数先把被乘数乘出来结果,写下来第一行。接着,拿着乘数的下一位把被乘数再一次乘出来,写在第二行上,但是要往左边移一位(这是因为实际上乘数不是一个个位数,而是一个十位数,所以,最后的结果要补一个0)。如果乘数还有百位,则继续这个过程,写下下一行,记得做相应的移位。最后,把得到的各行相加,用上面的加法的计算规则。
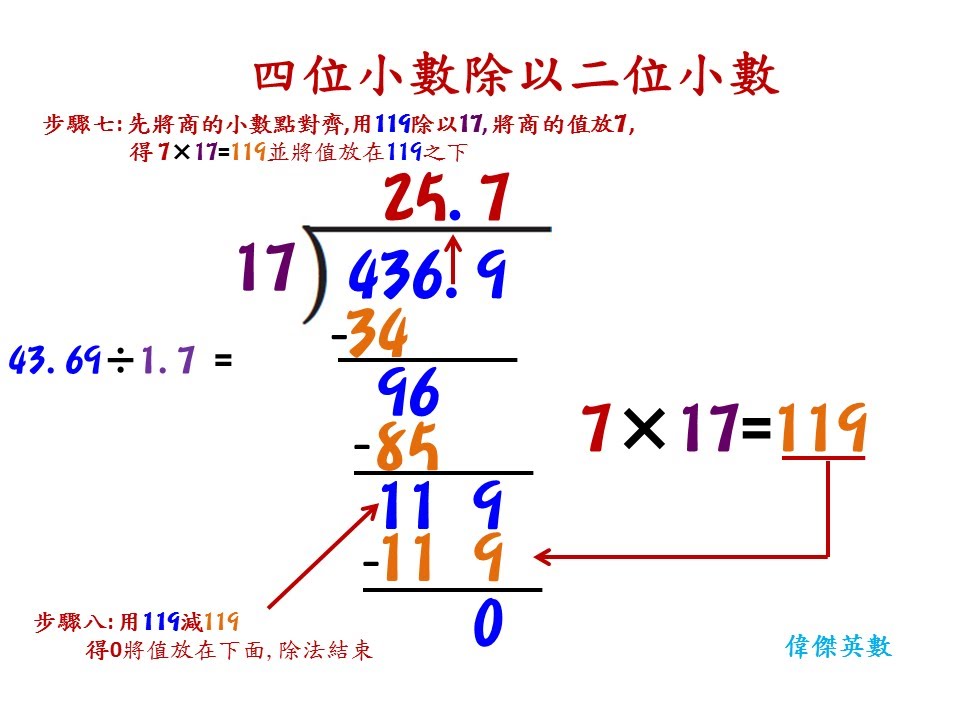
除法的计算规则:首先,把所有的计算转化成为整数的计算,这个时候被除数和除数分别被成了几次10要搞清楚,将来要把这些个10都除回去(当然,实际上只需要知道两者的差,如果被除数被乘了更多的10则将来要除以多出来的次数;如果除数被乘了更多的10则将来要乘以多出来的次数。或者,更简单的办法,把被除数和除数同时乘以同样数量的10,尽管这样会造成有的数后面有很多个0,但是商不变,将来也不用除回去了。实际问题中,用哪一种没关系)。接着,把被除数的第一位拿出来,让除数来除除看,按照情况写上(0,1,2,3,4,5,6,7,8,9)当中的一个,这一步叫做凑数。凑完数之后,计算除数和这个凑的数的乘积,写在第一位数的下面。然后做第一位数和乘积的差。得到差以后,把下一位拿过来写在这个差的后面。然后,重复这个“凑数——乘积——差——拿下一位”的过程,直到用完所有的整数。当整数用完之后,还是没有除尽或者达到要求,则在“商”后面加一个小数点,同时在最后的差后面加上一个“零”当做下一位数字。接着再次重复这个“凑数——乘积——差——拿下一位”的过程。
总结一下,加法的计算步骤是:小数点对齐,算个位数加法,注意进位;减法的计算步骤是:小数点对齐,算个位数减法,注意借位;乘法的计算步骤是:变整数,算个位数乘法写相应的一行,算加法,最后调整小数点;除法的步骤是:变整数(可以用被除数和除数同乘来避免最后的调整小数点),“凑数——乘积——差——拿下一位下来”,添加“小数点”并同时加“零”,然后继续“凑数——乘积——差——拿下一位下来”。
就这么简单的规则,并且通用,适用于任何题型,不需要按照不同类型的问题来调整,例如考虑除数是个位数还是多位数的情况,例如考虑被除数还是除数比较大的情况。也就是说,就算是最无聊的纯粹机械式学习的内容,也需要做到越普适越好,不要增加太多特例,尽量一石杀所有的鸟。其次,还需要做到每一个步骤都是可理解的,有道理的,而不仅仅是传授规则。例如,我从孩子那里了解到,在除法中有一步叫做“小数点对齐”——天哪这是什么规则啊,仅仅在被除数是小数同时除数是一位数的时候,这个规则是正确的。其他的情况偶尔也有能够算对的,但是,对于乘法和除法而言,小数点对齐真的是一个没有必要(适用情况有限)又非常容易出问题的规则啊。尽量不要教那些在特殊情况下才对,或者才能够加快计算速度的规则,而是尽量教那些普适的规则。为什么要对小数除法,或者说所有的除法,做这么多的分类,然后制定每一种类型的规则啊。天哪,这是什么样的教学指导思想啊。
要不,你看下面这道题(来源于google检索到的某个课外教学机构),如果我把17改成170呢,1700000呢?为什么会有小数点对齐这个规则啊?所有做题型教学的老师,我吴金闪今天向你们发出挑战,我认为所有的题型教育都是培养SB的教育。当然,在明白是什么,有什么关系,关系决定什么计算之后,做一定量的练习来熟练,我不反对。但是,我反对人为总结出来一些适合特定题目的计算规则,例如我听说过的各种各种的速算(什么末位数都是5则怎样,末位数加起来是10则怎样),那都是在误人子弟,而且是禁锢人思想,限制人思考的,最狠的那种误人子弟的方式。你看看这个题尽然还有步骤八,难道老师看不到就是在不断地运用“凑数——乘积——差——拿下一位下来”这么一个简单的规则吗(偶尔还会用到:整数用完的时候给商加个小数点,同时给被除数增加一个零)?
希望这个总结能够对小学数学的规则教学有一点点启发。这个实在是太恶心了,太低级了。不过,如果这个低级的任务不解决,将来更高级的内容有可能会出现更多的问题。当然,我这么说不表示我们就应该在这个低级任务上花费太多的时间,因为实在不行,将来也还可以用计算器、计算机、搜索引擎和机器人来完成这些低级的任务,只需要知道在什么情况下,根据什么关系,用什么样的计算。但是,尽量把规则总结好,理解好,使得规则说得通,还能够具有普适性,还是有必要的。
为什么不能按照题型的方式来分类然后总结,最后教学?为什么我痛恨这个?我们培养学生是在为了二十和三十年之后做准备,甚至是为了培养在二三十年之后会承担培养那个时候的二三十年之后的人做准备。我们自己都不知道那时候会怎样,我们如何为他们准备呢?他们的世界,他们遇到的问题,肯定会和我们不一样。当然,我以后遇到的问题也将和我现在的不一样。那么,我们如何准备呢?如果我们的方式是把现在遇到的各种问题做一个分类,做好解决问题的模板,然后希望将来他们能够用上这些模板,则是完全没有意义的。不久的将来,所有已经有答案的问题的解决都会被机器替代。我们希望的是将来他们喜欢并且能够提出和解决新的问题。这个时候,分类总结和记忆查询,就不再是面对新问题的方式了。只有教会遇到问题怎么去想,怎么去面对,例如愿意甚至喜欢面对新问题乃至发掘新问题,例如学会那些大概来说那些比较通用的普适的层面的思维方式和分析方法,才有可能有帮助。每一个学科,都要重新去梳理,这样的思维方式和分析方法,也就是我称为学科大图景的东西是什么,用什么样的例子来体现,怎么教,才能真的为他们做好准备。

