首先,了解投入产出:Input-Output Analysis Foundations and Extensions by Ronald E. Miller and Peter D. Blair.
其次,了解PageRank:The PageRank Citation Ranking: Bringing Order to the Web by L. Page, S. Brin, R. Motwani, and T. Winograd;Google matrix analysis of directed networks by Leonardo Ermann, Klaus M. Frahm, and Dima L. Shepelyansky。
接着,了解科学学:Bibliometrics and Citation Analysis: From the Science Citation Index to Cybermetrics by Nicola De Bellis
接着,了解流平衡分析和系统生物学:Systems Biology: Properties of Reconstructed Networks by Bernhard Ø. Palsson,What is flux balance analysis? by Jeffrey D Orth, Ines Thiele and Bernhard Ø Palsson
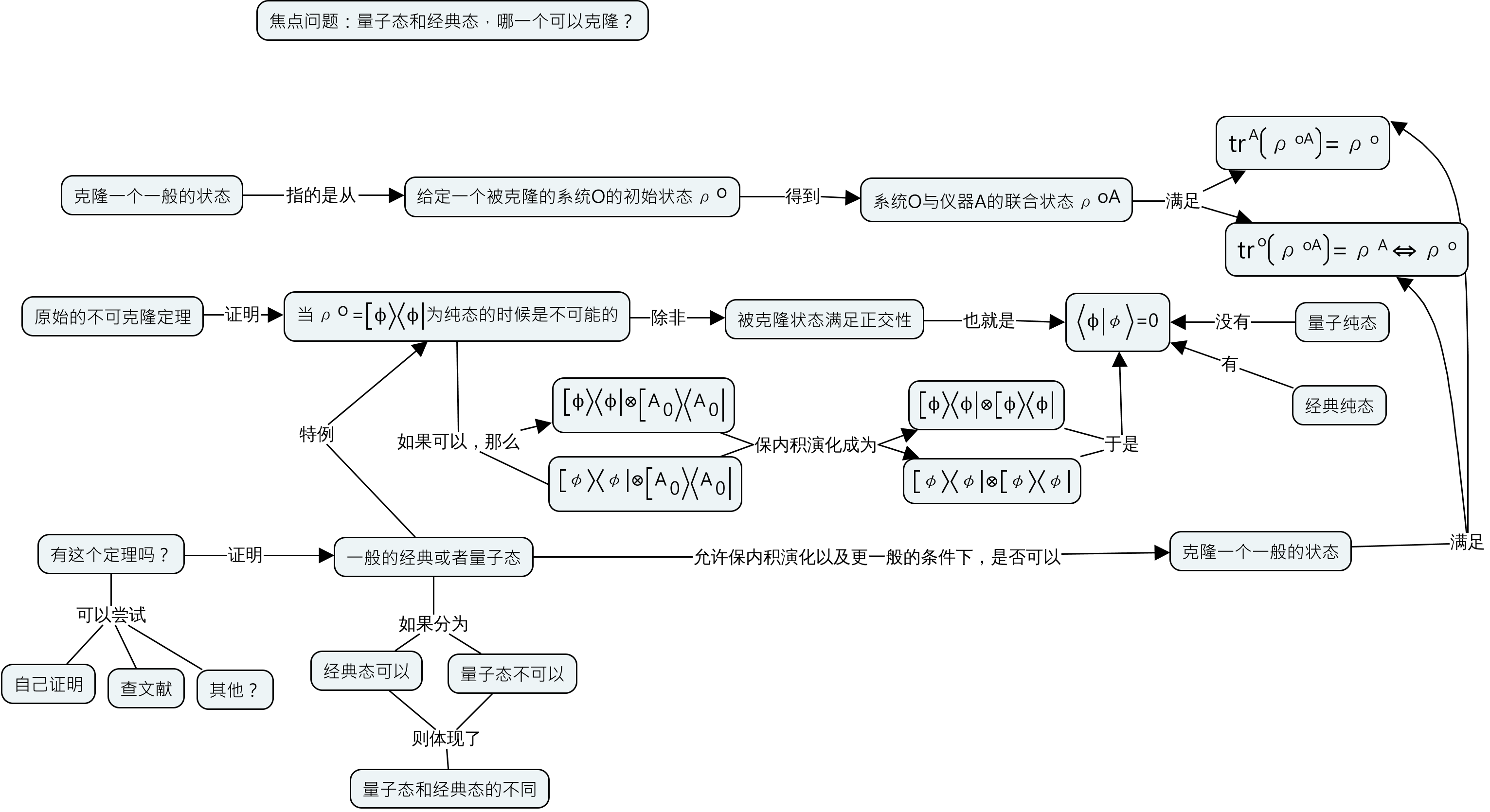
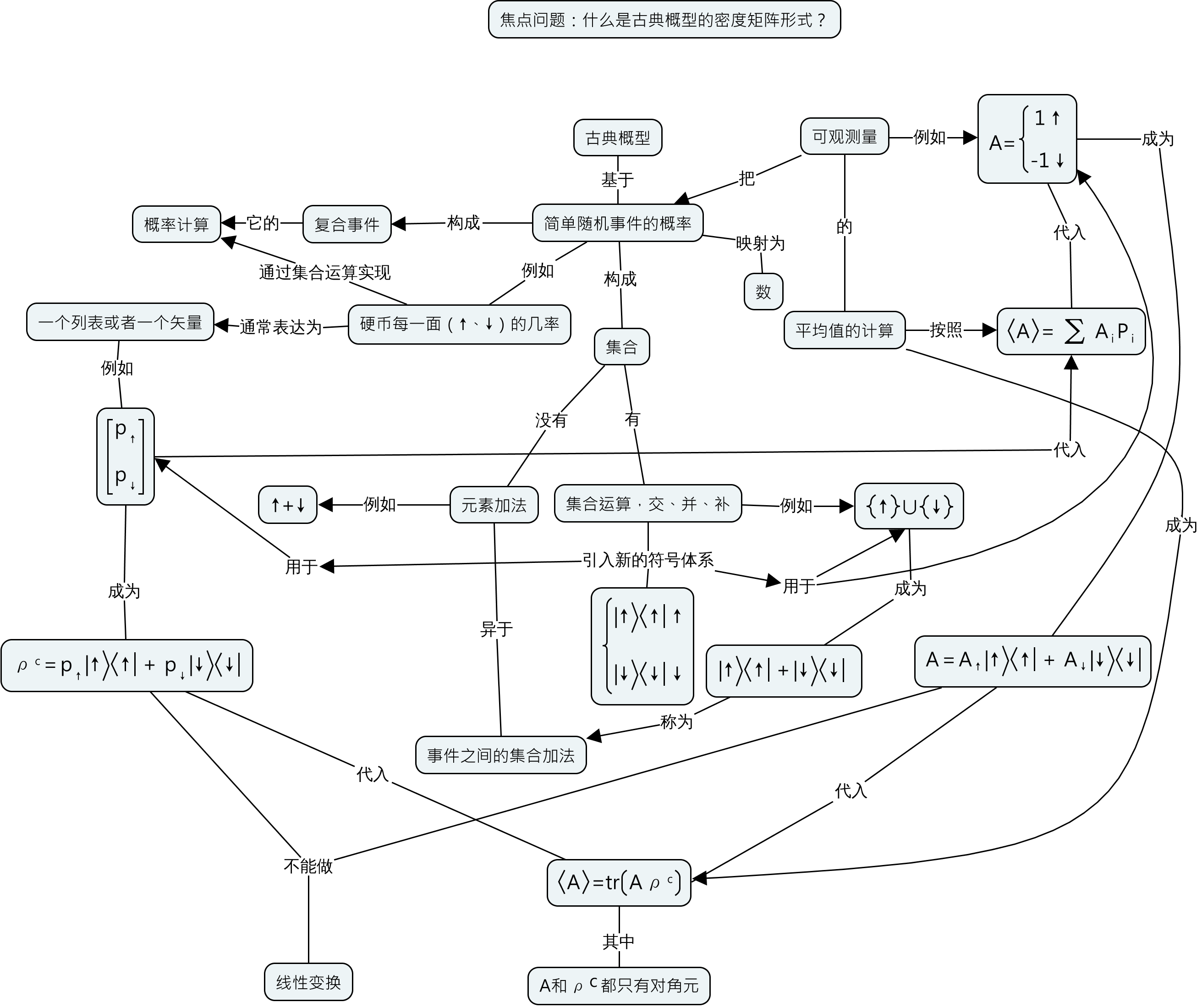
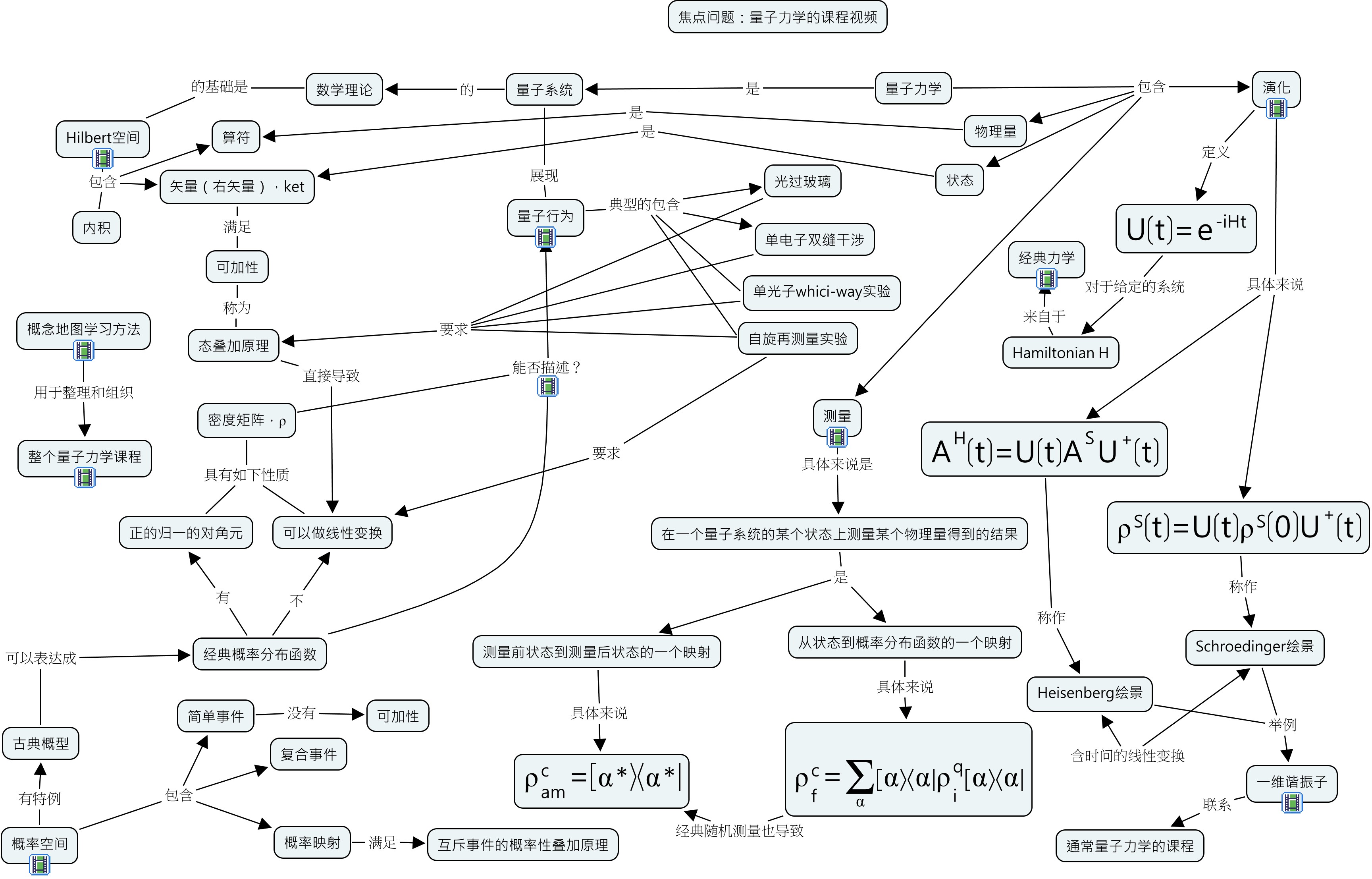
最后,几个领域连通起来的视角(前面的所有的准备就是为了能够明白这个):PageRank: Standing on the Shoulders of Giants by Massimo Franceschet,Spectral Ranking by Sebastiano Vigna,吴金闪的广义投入产出分析和细节投入产出分析,投入产出矩阵分析的主要思想小结,以及吴金闪的报告《广义投入产出分析》。
所有的知识的学习的出发点都可以是Wikipedia和google。
在理解和了解这一基本思想和这些学科的基本研究问题之后,可以思考如何用这个思想来解决这些学科的基本问题,以及还可以用来解决其他哪些问题(注意,我们的汉字学习的工作——Efficient Learning Strategy of Chinese Characters Based on Network Approach——实际上也是这个思想的一个应用)。
争取以后每一个领域,我都整理出来基本文献,供后来人使用。
刚才学生问,做什么样的研究。研究工作只有两个目标:顶天(最高深最核心的学问)、立地(最具实际性的学问)。如果还能够从立地的问题中提炼出顶天的来,或者把顶天的用于立地 的,就更加有意思了。其他的,不解决这两个问题以及它们的联系的学问,都不是学问,比如大多数研究者跟在人家屁股后面的工作。可借鉴,不跟从,要么钻研深刻的理论核心问题,要么解决实际问题中能够用非平庸的数学结构解决的问题。
学生还问,为什么我从来不直接给答案。当学生或者其他意图学到东西的人问我一个问题的时候,我通常会问更多的问题,意图是:搞清楚学生的根本问题在哪里,铺设台阶引导其思考,逼迫学生思考背后的原因然后能够做到举一反三。如果学生的答案有错,我也不会告诉他错了,而是沿着他的思路,问更多的推演的问题,然后让学生自己意识到答案的问题。这样做,学生能够得到的收获会更多。但是,大部分人都不是客观的思考者,会觉得我顺着思路把他逼到墙角,是不可接受的事情,于是,所谓的自尊伤害了思考。当然,这也是物理学家的问题,很多时候,他们把所有的问题简单地当做科学问题,分不清楚生活问题和科学问题的界线,搞不清楚学生的自尊和搞清楚问题有什么关系。这个也只能提醒自己一下,一不小心,就又忘了。