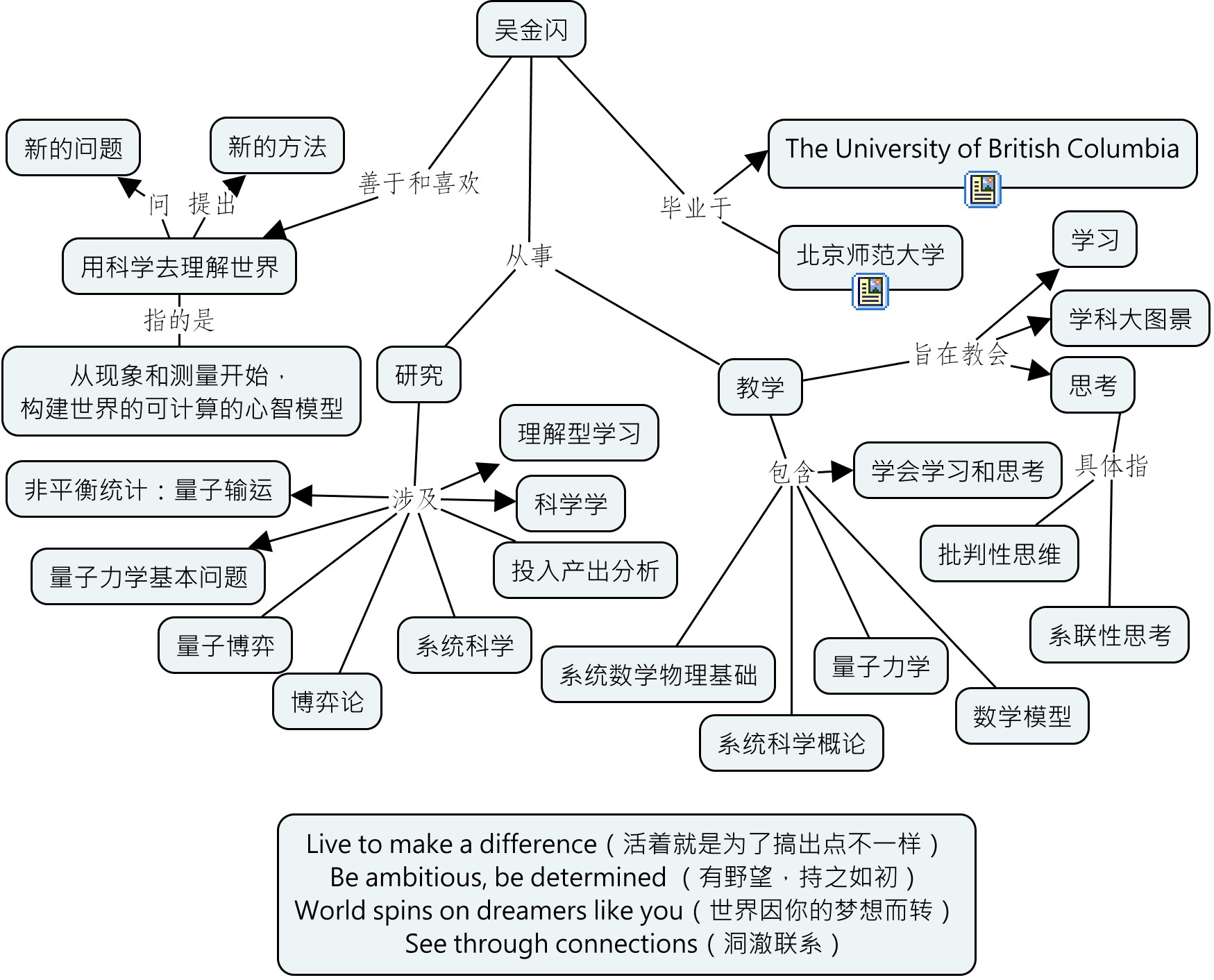
之前我们讨论了能够在很大程度上说明光是粒子的实验:光电效应为什么能够证明光的粒子性。那当然,也有大量的实验佐证光是波——把光看作是介质上的振动,然后依赖介质上的Newton力学来理解光的行为。那么,为什么光不能就是这样的东西:在解释不同的实验的时候用不同的模型呢?这样有什么不可以呢?
首先,有其他实验可以很大程度上证明光的传播不需要介质。例如Michelson-Morley实验(请自行Wikipedia之)证明如果有介质并且这个介质的运动速度通过伽利略变换进入光的传播速度的话,那么,实验结果和理论结果不符合。再例如,有实验证明光是可以在真空中传播的:你想确认一下这个事实的话,只要看一下天空,看到太阳月亮星星就是这个证明——你想中间有多少什么都没有的路光要走啊。当然,你仍然可以怀疑说,这个看起来测量起来什么粒子都没有的“真空”其实不是真空,还是有某种介质的。于是,你就可以设计一个情景来让这个“介质”有自身的速度,这时候,再来测量光的行为,就回到了Michelson-Morley实验。因此,Michelson-Morley实验很大程度上说明:光的传播不需要介质,如果有介质则这个介质很神奇——其自身运动的速度不怎么影响光的传播。
既然没有介质,那么,把光看作介质上的振动,并且这个振动的传播符合Newton定律就不太行了,那怎么来建立光的心智模型?
接着,我们回顾一下那些启发了光的经典介质波的模型的实验。例如,光的折射和反射。声波、水波都会出现折射和反射,也就是一个振动传过来遇到了界面,界面上的介质会被这个传过来的振动激发,由于是不同的介质,这个受激发的振动可能会被传播到其他方向上去。如果是同一种介质,其实也会发生这个受激发振动的事情,只不过,那个时候,跑向各个方向的受激发振动刚好相互抵消。而当存在不同介质的界面的时候,某些方向上的振动会被加强而不是相互抵消。这个把介质上的多个粒子受激发振动看作新的波源然后做叠加的做法叫做惠更斯-菲涅耳原理(其本质还是波的Newton力学),或者去看看Feynman的《QED:光和物质的奇妙理论》。当然,其实,光的折射和反射也可以用直线传播的小球和半透膜的模型来解释:把光看作小球,每次遇到半透膜(开了很多小孔的筛子?)就有可能被弹回,也有可能透过。这个称作光的随机性粒子模型(有的时候也被称作几率波粒子模型)。
那我们再来看光的干涉和衍射。衍射现象是指,在光的传播路径上,有障碍物,可是,你仍然在障碍物的后续路径上观察到了光。如果光是直线传播的小球,就不太可能有这个现象了。而波的惠更斯-菲涅耳原理就可以解释这个现象,在此略过这个解释。光的干涉现象是指来自于两个振动源的光在同时能够达到的区域会出现暗条纹和明条纹。暗条纹的意思是,对于打开任何一个光源就能够照亮的区域,当同时打开两个光源的时候,反而不变暗。当然,这个时候,对光源有一定的要求。但是,这件事情用光的粒子模型是很不可理解的:你在玩植物大战僵尸的豌豆射手或者用机枪打仗,发现,有一个地方用一个豌豆射手或者一个机枪手都可以打到,但是,当你放上两个豌豆射手或者两个机枪手的时候,就打不到了。这是不可能的事情。如果是这样,就没有火力覆盖了。
那么,把光看作是介质上的振动是怎么来理解光的干涉的呢?说一个光源传过来的振动和另一个光源传过来的振动可能在振幅上不匹配,例如一个是振动最低点也就是波谷的时候,另一个正好传过来一个振动最高点也就是波峰,正好这两个振动的矢量叠加相互抵消,于是,没有照亮。这个解释非常漂亮。
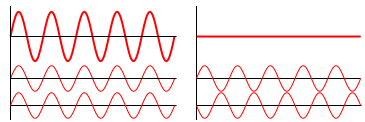
那问题来了,到底我们应该把光看作是粒子还是满足Newton定律的介质上的振动波呢?我们能不能在讨论某些实验例如折射反射光电效应的时候,把光看做粒子(当然,这时候,我们也要问这个粒子是不是满足粒子的Newton定律。问题留在这里,以后再说),而在讨论折射反射衍射干涉的时候,把光看作是满足Newton定律的介质上的振动波呢?万一遇到新的现象怎么办,用什么方式来描述?或者每次都先试试用两个理论之一的结果和实验比较一下,对上了,对这个现象就用这个理论?
第一、科学的目标是希望对于给定的现象,我们的理论模型能够给出来一个结果的预期,然后和实验相比较。因此,每次来凑一凑试一试显然是不行的。如果能够对现象做一个完善的分类,遇到现象就知道用哪一个模型,倒是也可以接受。不过,这个分类,在光这个现象上,我没有见过。
第二,科学的原则有一条,希望用更少的并且相互不冲突的更具有一致性的理论来解释更多的现象。因此,用两条看起来相互冲突的理论来解释同一种东西的不同的现象是不够的,就算上面提到的完善的分类存在的话。而且,将来,我们会看到,有一个光的新的理论,它能够同时解释上面所有的现象。
顺便,我们怎么知道是同一种东西呢?只要我们做实验的时候产生光的机制是一样的,然后用来做以上两类实验就可以。另外,在这里,我特意扔掉了光的波的模型,而用更加复杂的“满足Newton定律的介质上的振动波”的模型。将来我们会知道新的模型还是一个光的波的模型,只不过不符合Newton定律,而且是振幅波,而不是几率波。后面为了语言的简单,我把这个“满足Newton定律的介质上的振动波”的模型简称为经典波模型。
那么,到底怎么办?什么样的模型可以即具有粒子性,也就是确实是一颗一颗打过来的,不会再一次把能量分离成为某个最小单位以下的,强度增加就意味着增加粒子数量的,这样的粒子,还具有波性,也就是可以发生干涉和衍射的这样的波?
再一次提醒注意这个干涉的不可思议性:如果我们用一颗一颗粒子来解释的话,就意味着有一个地方打开两个粒子源中的任意一个粒子源的时候粒子能够到达,但是同时打开粒子却不能达到。
更进一步,这个实验还可以这样做:保证在整个实验中每次仅有一个粒子,也就是一份能量,在整个实验环境中。具体的做法大概来说是这样,制备一个单光子光源,在这个光子的光路上放上分光的仪器使得这个光子可能走两条路中的一条——例如放置一个双缝或者一个偏振分束器。
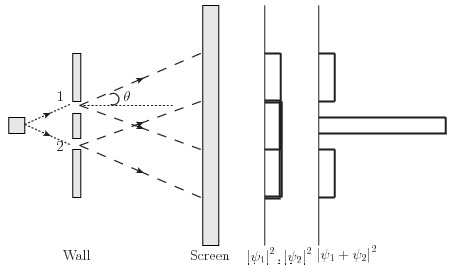
这样来做,这个实验结果就更加不可思议了:空间中每次只有一个粒子,如果说不能到达某个一条路就能到达的点,也就是说,好像这两条路上的光子影响了彼此,可是,真的仅仅有一个光子啊,自己和自己是怎么影响怎么抵消的呢?回到波的模型,可以把波看作是振动分成几个部分传播到不同的路径上,将来再一次合起来,自然就可以相互抵消。可是,光子不能再一次分成更小的能量单位啊!
注意,把光看作几率波的模型也不能解释这个单光子干涉现象:要么走路径1,能够到达;要么走路径2,还是能够到达,则合起来就是能够到达,绝对不会出现不能到达的情况,除非路径1和路径2的“几率”是一个矢量,能够想振动幅度一样被加起来。
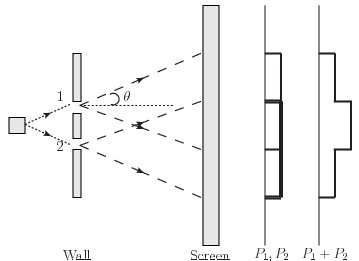
这里最大的矛盾,或者说将来的出路,就在于:一方面,光子不能分成更小的单位,不能同时走很多条路径,因此不能把不同路径上的“振动幅度”像经典波一样叠加起来;另一方面,在数学上,经典波的把来自于不同路径上的同时传播过来的波相互叠加起来,确实能够描述实验现象。
怎么办?难道我们需要一个在数学上满足“波的叠加”的但是在物理上是一个个不可再分的小球的模型来理解光子的行为?一个个的小球怎么会具有波呢?除了看作概率,就像前面的半透膜,可是概率解释不了干涉,还可以看作波,怎么可能呢?
实际上,光的心智模型正是这样的满足“波的叠加”的小球。有更多的实验会提出来挑战很大程度上说明,只有这样的模型,才能够解释这些实验现象。例如,这几个实验:
能看到光是多么神奇的事情啊
光过玻璃是一件多么神奇的事情啊
光过三个偏振片和男人女人过三道门的对比
Feynman说过,只要你能够明白双缝干涉,那么,你就明白了量子力学,并且如果你没有被量子力学苦恼过,那么,你就是不明白量子力学,更有你只要宣称明白了量子力学,那么,你就没有明白。
学习量子力学主要就是为了搞清楚为什么这个理论是这个样子的,理解上的主要困难在哪里,而不是仅仅学会怎么算。就像Feynman在《QED:光和物质的奇妙理论》,《Feynman物理学第三卷》以及吴金闪的《二态系统的量子力学》里面所强调的一样。怎么算,不好意思,你需要至少学习一个理论物理专业的硕士,甚至博士。
具体现象的知识固然有意义,但是,本文最大的目的是跟你一起从具体的科学现象的思考中体会什么是科学,体会量子力学的神奇和困难之处。