上课做了一个实验之后,学生说:这个实验以及您提出来的问题迫使我们做深入的批判性的思考,但是,从这个思考的结果看起来,我们之前对于光过一片玻璃,而不仅仅是这个实验中为了展示神奇之处用的三篇玻璃,的理解,也是有问题的啊,因为一个好的理解应该能够解释所有的这些现象啊。是的,说得很好。这个例子也会找时间写出来。今天我再举一个光过玻璃的例子。这个例子来自于Feynman的《光和物质的奇异性》。
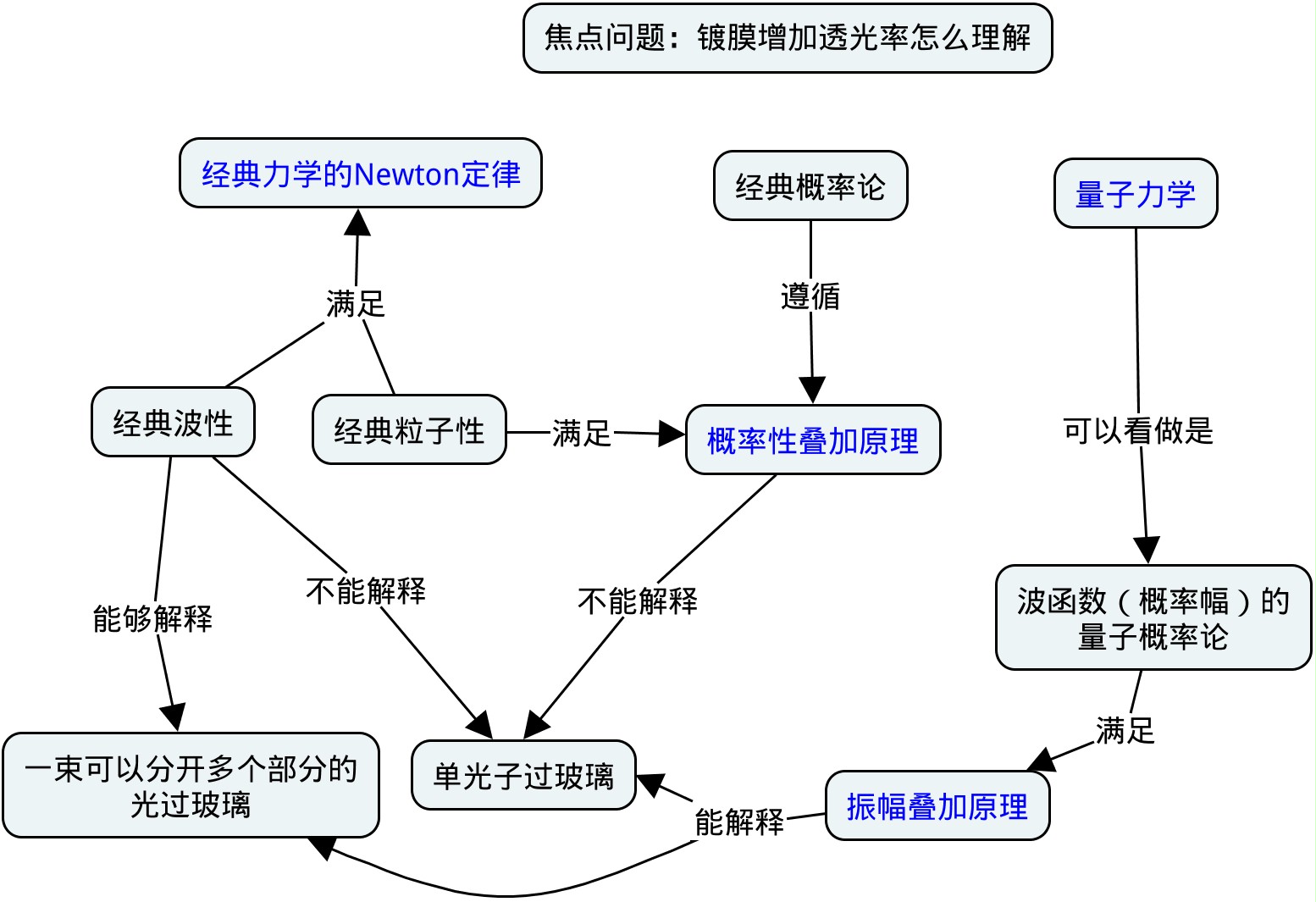
大家都见过相机镜头。你会发现一般来说镜头是有颜色的。这个颜色来自于镀膜——给相机玻璃上增加一层其他材料。其主要目的是增加透光率。有的时候是所有颜色的光的透光率,有的时候是为了增加某些颜色的光的透光率。现在,问题来了,为什么增加了一层膜之后,会增加透光率呢?
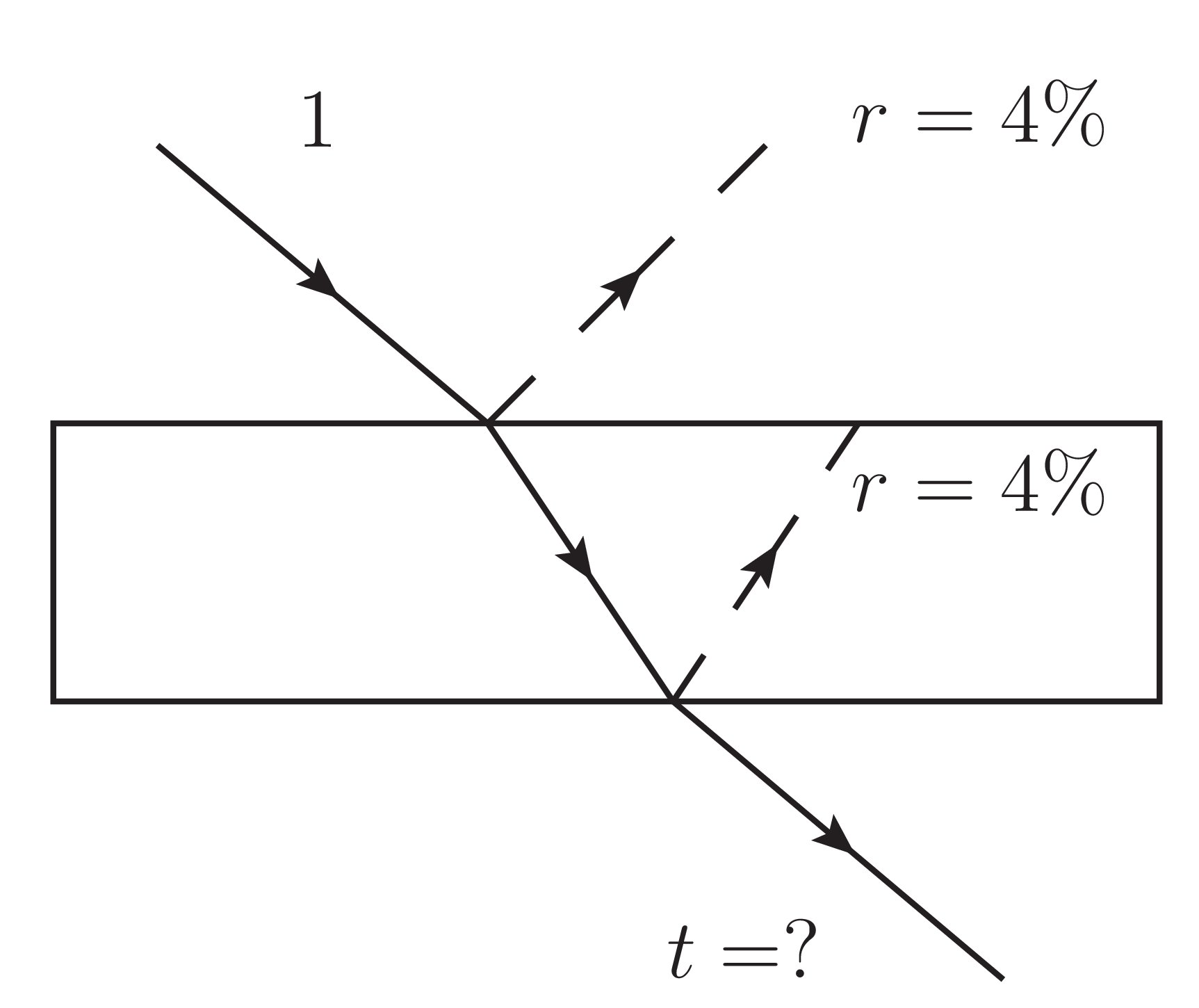
按照我们日常的体验,或者中学学过的光的反射和透射,我们知道每增加一个界面光就会发生反射。于是,我们粗糙地假设每一个界面\(4\%\)的光会被反射走。那么,能够通过第一个界面的光就是\(96\%\)。接着,这个\(96\%\)的光会通过下一个界面,继续发生反射,大约又会有\(4\%\)的光被反射走。于是,经过一个玻璃或者膜的两面之后,通过率会差不多等于\(92\%\)。按照这个图景,增加的膜越多,则透过的光越少:你看,就像一个小球打过来,每次都要反射走一部分啊。或者说,这个图景实际上是把光看做一个个服从概率理论(具体指的是独立事件的乘法——如果一件事情有前后两件独立的事情组成则这件事情的概率是那两件事情的概率的乘法,和互斥事件的加法——如果一件事情有两种完全排斥的可能发生的方式则这件事情的概率等于这两个方式的概率相加)的小球。这样的服从概率论的经典小球的模型你是深有体会的。那么,这样的模型能不能用来理解光过玻璃呢?不行。如果这样的话,通过镀膜增加界面是不可能增加透光率的。那怎么办?
为了更清楚地展示这个模型的困境,我们来看如果一个一个小球打过来,会怎样。任何时刻,我们保证整个空间只有一个小球。这是做得到的,通过使用一个叫做单光子光源的仪器。现在,我们来看这一个小球。先到达第一个界面,假设被弹走了,故事结束。这个可能性是\(4\%\)。假设透过了第一个界面(这个可能是\(96\%\)),现在来看这个小球到达第二个界面时候的情况。这个时候还是有两种可能,透过了,故事结束。这个可能是\(96\%\times 96\%\approx 92\%\)。如果弹走了(这个可能是\(96\%\times 4\%\)),则故事差不多结束。这里“差不多”的含义是实际上,我们还应该考虑多次的反射。不过为了简单性计,就不再计算了。
经典波动光学是这样来解释的:把一束光看作是好多好多小球合起来构成的,或者是介质上的振动形成的。我们先来看好多好多小球合起来的视角。说,到达一个界面的时候,我们把小球们分做两部分,一部分弹走,一部分进入玻璃。对于进入玻璃的那一部分,在第二个界面还是会分成两份,一部分透过整个玻璃,一部分回弹到第一个界面。对于回弹到第一个界面的那部分,其中的大多数小球会透过第一个界面出去,和那些第一次就被弹走的小球们合在一起。当合在一起的时候,不知道什么样的原因,这两部分小球就会有相互干扰,例如相消,于是,整体反射光减少。所以,能够只能通过透射光出去,于是透光率增加了。在这里,神奇的地方就在于:你如何让两束光里面的小球们相互影响?光的这些小球们很独立的,基本上不发生相互作用。因此,这个很多个小球的模型不是一个好的模型。
再来看介质上的振动的视角。介质上的点的振动之间确实时会发生影响的:一个点的振动会带动附近的其他点的振动,并且如果有两个振动源的效果传到了同一个点上,则这个点的振动应该是传过来的两个效果的矢量叠加。为什么是矢量叠加?因为这两个点的振动传播过来的方式符合牛顿第二定律,而这个定律是矢量形式的:哪个方向上有里的作用则那个方向上产生运动的改变。这样来看,我们可以很好地理解前面的这个透光率增加的事情。实际上,这个现象有一个名字,叫做光的干涉。具体来说,是这样的。一束光在第一个界面分开成两束,反射和投射。反射的光就好像是从界面上的反射点开始的一个往玻璃外面的空间传播的介质波。透射光呢就是往玻璃内部传播的介质波。接着,透射光遇到第二个界面。这个时候,再次分成两束。第二次投射的那部分不用管了,故事结束。在第二个界面上发生反射的那部分的那部分光就会回到第一个界面,而且其中的大部分会透射到玻璃外面,和第一次反射的光可能会到达同一个地点。这个时候,在这个同一个目的地上,就会发生来自于牛顿第二定律的矢量叠加,于是,发生相消(或者相长)的事情。可是,这个解释有一个很大的问题,光子不是介质波,其背后没有牛顿第二定律,没有矢量性。怎么办?
我们已经看到了,经典单个小球的模型不能解释增加透过率这个事情,经典多小球模型也不行,经典介质波模型也不行。我们再来看看量子力学又怎么解释这件事情。
量子力学是这样来解释这个问题的。还是假设我们每次在整个空间中只有一份光的能量,称为光子。量子力学问,光子反射回去这件事情有集中发生的可能啊?第一种,第一个界面就发生反射。第二种先在第一个界面发生透射,然后在第二个界面发生反射,接着回到第一个界面发生透射。无脑量子力学说,凡是这样的一件事情有两种“不可区分”(大概来说就是问,如果你在玻璃的第一个界面的外面观测到一个光子,你能够知道是第一种还是第二种方式来的吗?不能就是不可区分。实际上,精确含义更加复杂)的方式发生,则需要把这两种方式(的概率幅,而不是概率)做直接相加。这个时候,你只需要算一个相加得到的概率幅对应的概率,自然就得到既可以相消也可以相长的结果。
但是,你仔细想,这个事情还是很神奇啊,还是有问题啊。你看,只有一个光子的情况下,第一个界面就反射走的光子,有怎么会“遇到”并且“影响”,那个先透射再反射再透射的光子呢?整个空间只有一个光子啊!于是,只要第一次被反射走了,那么,后面的事情就不可能发生了,那怎么相互影响相互遇到啊!如果说,第一次没有被反射走,则整个空间的唯一的光子也就只会发生后面的两种可能啊,不可能再和那个从来没发生过的第一次就被反射的光子来相互影响啊!怎么办?
然而,量子力学的神奇之处就在这里:只要一件事情有两种发生的可能,这两种可能还不可区分,则整个事情的概率幅等于两种方式的概率幅相加,接着概率相当于概率幅的绝对值的平方。通过这个先相加后做绝对值的平方,我们就能够得到和经典介质波数学上一样的矢量叠加的形式。
下面的公式就表示了这个意思,尽管根本没希望读者们真的看懂:
\begin{align}
\rho^{c} = p_{1} \left|1\right\rangle\left\langle 1\right| + p_{2} \left|2\right\rangle\left\langle 2\right| \\
\rho^{q} = \left(\sqrt{p_{1}} \left|1\right\rangle + \sqrt{p_{2}} \left|2\right\rangle\right)\left(\sqrt{p_{1}} \left\langle 1\right| + \sqrt{p_{2}} \left\langle 2\right|\right) \\
= p_{1} \left|1\right\rangle\left\langle 1\right| + p_{2} \left|2\right\rangle\left\langle 2\right| + \sqrt{p_{1}p_{2}}\left(\left|1\right\rangle\left\langle 2\right| + \left|2\right\rangle\left\langle 1\right|\right)
\end{align}
前者表示\(1,2\)两种方式按照各自的经典概率\(p_{1},p_{2}\)来相加,后者表示这两种方式按照其概率幅(大约可以看做其开平方\(\sqrt{p_{1}},\sqrt{p_{2}}\))来相加,然后再求其绝对值平方。这样就会多出来最后那个括号里面的额外的项,而它们就是那些导致相消或者相长的部分。
通过这个例子,我想体现——哦,这个任务交给读者。记得去使用WHWM,问传达什么信息,如何传达,为什么这个信息,为什么这样传达,对我有意义的我喜欢吗,这几个问题。同时也可以去看前一个帖子“能看到光是多么神奇的事情啊”的总结。