分类： 教学思想和技术

昨天“机器人能够取得高考好成绩意味着什么？”的帖子引发了老师们的讨论。问，那到底要教什么，怎么教呢？事实性知识我们学不过AI，甚至连AI的设计者学不过AI，程序性计算分析的知识我们也比不过专门的软件，我们到底学什么？

帖子里面说了，面对现象、提出问题（把问题变成自然语言，然后更进一步变成数学语言或者某个学科的语言的形式）、解决问题是学习的目标。事实性知识本身不是学习的目标。除非，其被用于面对问题、提出问题和解决问题。那么，到底如何来教大家面对问题、提出问题和解决问题呢？甚至有老师问，如果没有事实性知识当基础如何来解决问题呢？

关于事实性知识是不是应该有的问题，请参考“你能够倒背《史记》如流吗”的讨论。不是说事实性知识就是毒药，而是说，如果学习的目标就是事实性知识那么，就是毒药，起到的是限制你思考的作用。我说过有的人认为“面对问题、提出问题和解决问题”是第六个馒头，“事实性知识”是前五个馒头，不吃前五个，第六个没法直接吃，也不能吃饱。这是完全错误的。如果我们上来就围绕着这个第六个馒头来设计教学，尽管没准还是要铺垫一个馒头，但是至少不会需要先连吃五个——早就吃腻了，吃吐了。就这样一个简单的逻辑，我不知道为什么就有人非得说前五个馒头很重要。真的，它们不重要，除非它们正好可以来帮助你吃好和消化好第六个馒头。那么，教学中的第六个馒头到底是什么，怎么教？

从馒头这个目标来说，就是每一门课程的大图景：典型研究对象、典型问题、典型思维方式、典型分析方法、和其他学科以及世界的关系。从吃馒头的过程来说，就是需要让学生来体验面对问题、提出问题和解决问题的经验。其实也就是下面这几个关键词：学科大图景、理解型学习、系联性思考、批判性思维、做中学、以项目或者问题为基础的教学。

有老师说，让我举个例子。在课程设计上的例子，可以看例如我们的科学和科学教育的课程设计、“学会学习和思考”的课程设计原则。也可以看下面的一张概念地图：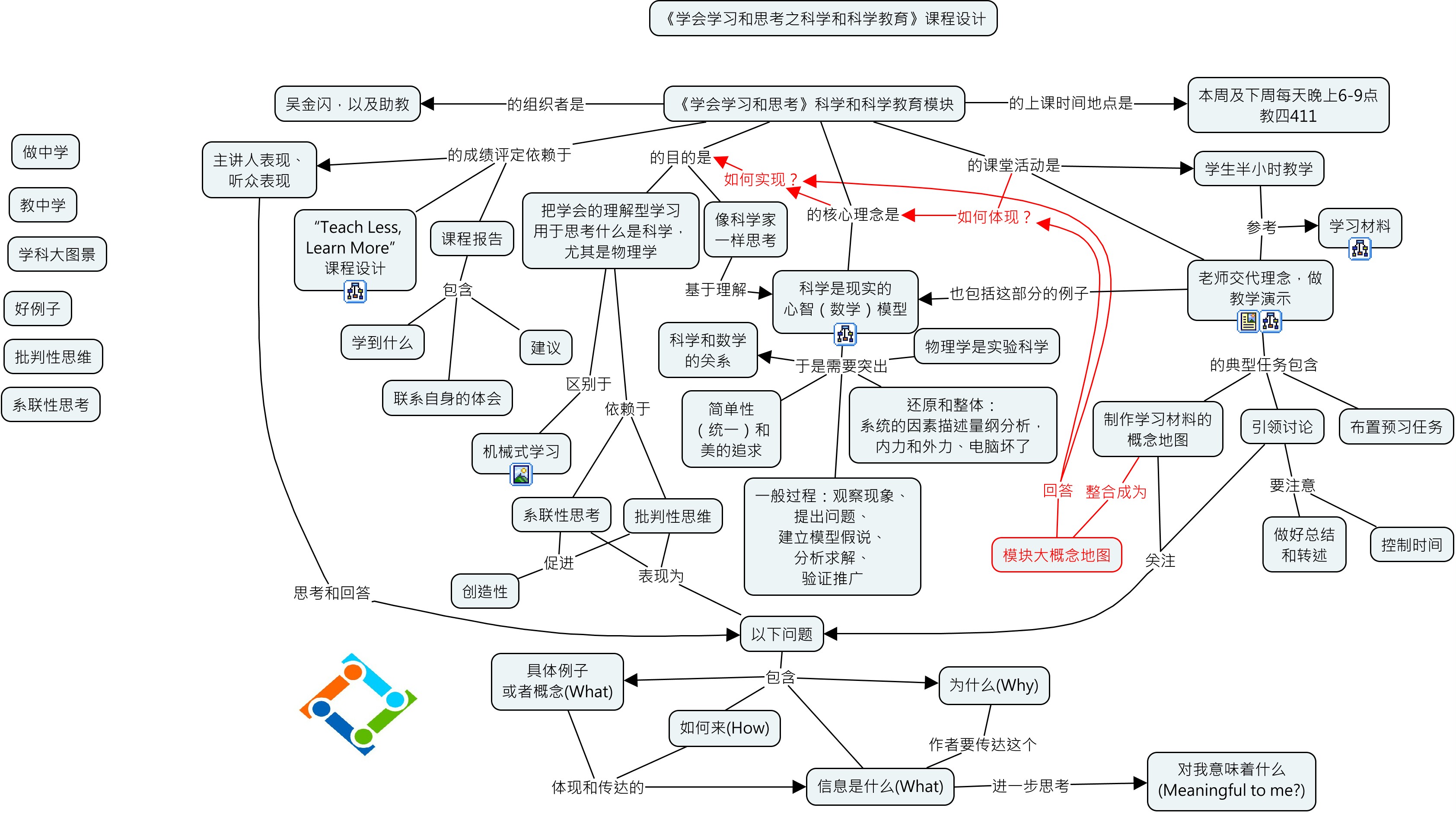

在具体怎么教环节的例子，可以看在“你能够倒背《史记》如流吗”两个例子的对比：六个馒头的问题和钢琴的八度之间有几个黑键。

在第一个例子中，孩子没有学过除法，甚至连减法也没有正式学习过。这个时候，当我问，六个馒头，每天早上吃掉三个，可以吃几天的时候，孩子就是通过思考这个过程来解决的：竖起来六个手指，然后每次摁掉两个，问摁了几次，发现三次。而且更加宝贵的事情是，第一次思考了很长时间以后，给了答案，却告诉我，“我忘了怎么想的了”。这说明，肯定是当场想起来怎么解决的，而不是之前就会了的。如果仅仅从答案是否正确的角度来说，当然，学习了除法就更快更准确。但是，学习数学是为了学会用数学来思考，而不是学会做四则运算！这是学科大图景的问题。把问题转化成一个数学问题，然后在尝试解决。甚至转化这一步比解决还要重要。而这样的东西，如果先交计算，再企图让孩子明白计算的用法，就完全学不到了。而且，更加悲惨的事情是，这个过程不可逆，一旦被教过计算，那这个用计算的含义自己来构建这个计算和计算的规则的过程就没有了，于是，也就失去了学会面对问题、提出问题的机会。

在第二个例子中，孩子除了依靠对钢琴的记忆，然后数数之外，基本上就不可能做到理解型学习。具体的这个问题的理解型学习的困难见“你能够倒背《史记》如流吗”。

当然，如果选择目前还真的没有答案的问题，一起来面对和研究，是最好的。但是，第一，没这么多合适难度的没解决的还适合学生的问题；第二，也不能对老师的要求这么高。那怎么办？我们可以把学科中的一些重要概念当例子，回到这个概念在提出来之前的情景，必要的时候给学生一点点启发，然后让学生体会这个概念提出的过程，让学生去痛苦，去失败，去成功，去快乐，去获得提出和解决问题的体验和信心。甚至，我们可以帮孩子们准备好求解问题的设备（例如AI、电脑、数学软件、google等等）或者直接帮孩子们求解问题，只要问题明确以后。这样，强迫孩子们把注意力放在面对现象、提出问题和提出大概的解决思路上，而不是实现解决过程。

这个过程其实不难，如果你有心的话，你可以把大量的知识的学习都变成这样的一个体验的过程，一个经历痛苦快乐失败成功的过程，一个需要创造性地运用学习者的思维的过程，而不是知识的灌输。有一个老师说，

有时候，没有“有意识”的心，就根本迈不进去。
有时候，迈了进去，没有“发现”的敏感心，就白走一样。
进去了，有了敏感的心，没有团队，就越走越孤单。
越走越孤单的时候，没有强大的内心世界，就等不到好结果的一刻。

说得很好。这样的实践者肯定不容易，肯定不如拿起一本书一本教材一套习题集来教的老师容易。但是，这个世界上绝大多数突破不都是要忍得住孤独的心、强大的内心世界、合适的方向、适合的能力，再加上不懈的努力来完成的啊。像“教学”这么重要的事情，其突破那更加就应该如此了。

这也是为什么会有这个公众号，有老师们的微信讨论群，有《学会学习和思考》的课程，有《教的更少，学得更多》这本书。

英国University of Surrey的Ian Kinchin有一篇文章标题叫做“Universities as centres of non-learning”（作为最不学的地方的大学）。不是说，教了包含微积分和线性代数甚至拓扑的高等数学就是真的高等级的数学了；不是说，教了最小作用量原理和相对论甚至量子力学的物理学就是高等级的物理学了；不是说，浏览和了解和更多流派的画作和技巧就是高等级的美术了，尽管我们的大学基本上就是在教这些。那么，到底大学在各个学科上应该教什么呢，有没有教应该教的东西呢？

我一直在批评，小学教的四则运算，不管多么熟练能够计算多么高位的数字，都不是数学。那么，难道大学教的高等数学就是数学了吗？如果这样，也简单，往前赶就行了：让小学把现在初中的教了，初中把大学的教了（高中干什么？全留给复习，准备应付考试好了）。那到底什么才是教真的数学，不管大中小学。到底什么才是教各个学科？

今天遇到两个例子。第一个是我《学会学习和思考》课程的老师Kip举的他儿子的例子。他说，他居住的小区经常有人开车比较快。他儿子及其小朋友们就想看看到底那些车有没有超速。如果有测量速度的仪器（例如多普勒仪，现在马路上测速就用这个？），这是很简单的。孩子们没有这个仪器，甚至连足够长的尺子也没有。这群小朋友是这样做的：先推动自行车，记下来某一段路滚了多少圈（在车轮上做一个标记，撞到地上就记一圈），然后量好了自行车轮子一圈多长；接着，拿着秒表来给经过这段路的车计时，就知道车速了。并且，可以尽量匀速地骑行自行车，先算好速度，这样将来只需要把两个时间除一下就知道比自行车快了多少倍。这就是数学：把实际问题转化为数学问题，把关系转化成计算、转化成数学结构，是数学。类似的例子，还有我家心儿对水果店做的统计（见我们的公众号“为了理解教和学”之“用数学来做发现思考和表达”）以及对自来水使用量和生产量的分析。当然，为了有素材，有结构可以用，学点已经有的数学结构是有必要的。但是，更加重要的是，学会把问题转化成已有的数学结构或者从问题里面构建新的数学结构，才是数学。当然，除了创设情景来理解概念或者定理地图的动机，把概念之间的关系把握好理解好，也是好数学。那么，其他学科的好教学也一样，需要去追问那个学科里面最典型的思维方式、分析方法、基本研究问题、和世界以及其他学科的关系是什么，然后围绕着这个大图景来选择好例子。

说完了好数学的例子，来举一个坏的例子。天津美术学院有一个叫“李宝玖”的学生发了一个退学申明，

由于觉得学不到东西而退学，很了不起。尽管其退学可能有其他原因，例如违反校规很长时间不上课，但是，如果忍忍还是能够获得学位的，还是能继续混下去的。这个看其所拍摄的视频就可以了解到，也可以看下面老师对李宝玖的评价：

回忆起这位学生在天津美院三年的经历，一位天津美院的老师这样说：“我了解到这个学生上大学的时候还是不错的，比较积极上进，希望以后在艺术上可以做些有影响力的事情，希望出人头地。”

我也不想具体讨论这个事情本身太多，尽管我也特别想了解美术教育到底教什么——是技法为主、欣赏为主、历史和流派介绍为主？我也不知道理想的美术应该以教什么为主。我想问的问题是，仅仅是美术教育学生从中学不到东西吗？数学、物理、化学、地理、文学、语言、经济、社会等其他学科呢？唱歌、书法、舞蹈等艺术类学科呢？我自己学过大量的数学和物理，在全球好几个不同的学校。我觉得还是能够学到东西的。学到的分几个层次：具体某个学科和某门课的知识，构成这个知识的概念和概念之间的关系，从这个具体知识开始产生的什么是数学或者物理这个学科的理解以及什么是科学的理解，甚至到学科的典型思维方式的理解，到解决学科发展的问题或者用这个学科来解决世界或者其他学科的问题的理解。因此，我认为，数学物理这些学科，还是能够从大学学到东西的，而且需要从很细节的很具体的概念和概念之间的关系抠起，同时心里要有这个学科是什么的大问题和对大问题的追求。当然，也不是每一门课都能够做到这样。例如，我学过数学老师开设的《量子力学》，其主要关注如何估计算符的本征值的上下界之类的问题，认为量子力学的叠加原理非常的平庸——你看不就是因为量子力学的基本方程是线性微分方程吗，自然你的解满足叠加原理。这就是属于只见树木不见森林。不过，人家本来就是这个方面的数学家，为了解决物理理论中的计算问题来的。

如果拿着这个标准来看其他的学科，我们问：某个学科或者课程有这个学科的大图景（对象、问题、思维方式、分析方法、和其他学科以及世界的关系）来当做教和学的中心吗？有把具体的概念、概念之间的关系等例子选择和精炼，来体现这个大图景吗？甚至，我们的大学教育的执行者们设计者们，有思考教什么的问题吗？还是在做无脑教学：拿过一本书，或者已有的一个培养方案，复制一下，从书上抄到黑板上或者PPT上，然后希望学生从黑板上或者PPT上转录到脑子里面，或者至少在考试的时候，还能在脑子里面？如果是这样，我们对得起来给了我们时间甚至敬仰的学生们吗？

看来源于同一个帖子的下一段话：

“十几年没见过你这样的学生”是片中杨书记无奈之下对李宝玖的评价。上课的时候，李宝玖也是老师眼里难对付的学生，老师正讲着课，他有时会当场质疑，“比如对于现代主义，我觉得一个二十几岁的人应该对它有一个反思，好好在哪儿，不好又不好在哪儿?不应该是直接灌输。”慢慢地，他在学校上课的时间越来越少。

如果学生当场质疑就是难对付，甚至需要对付的学生，咱们的老师们是在当老师吗，这是什么心态？老师说的就是对的？后面那句话“比如对于现代主义，我觉得一个二十几岁的人应该对它有一个反思，好好在哪儿，不好又不好在哪儿?不应该是直接灌输。”说得多好啊。反思而不是灌输，难道错了吗？这是多么好的学生啊。笛卡尔说，我从来不把没有经过我反复拷问的东西当做进一步思考的基础（大意）。科学就是反思和实验以及数学的结合才发展起来的。难道美术就不需要反思吗？

我不知道多少大学的课程实际上就是在灌输知识，并且这些知识也是没有考虑过为什么非得需要称为学习内容的知识。真希望有人能够搞一个调查，看看大学毕业十年二十年的学生对自己收到的大学教育的评价，看看这样的无脑教学有多少。

昨天和王晨光聊天，说起来“为什么实践理解型学习有难度”这个问题。首先，我们注意到很多人有做理解型学习的理念和期望，例如大家经常听说的“授人以鱼不如授人以渔”、“因材施教”。在我们宣讲我们做理解型学习的理念和实践的时候，我们也可以感受到，尽管对很多老师是冲击，但是，能够明白这样做并且希望这样来做的听众们很多。但是，其次，我们就注意到就算经过我们的培训（课程或者工作坊，甚至微信群）之后，能够把理解型学习在自己所教所学中用起来的人不多。这是为什么呢？

当然，第一人类还没有被逼到绝路上，记忆性学习、机械式学习以及靠其学到的知识成为一个博学的人或者考试成绩比较高的人，还算一个有意义的目标，还能混下去。再加上大多数考试确实可以通过做大量类似习题的方式来准备这个考试而获得高分。于是，以学习知识——甚至大多数时候是一筐子的像鸡蛋一样没有联系的孤立的知识之间以及和现实没有联系的知识——为目的的机械式学习就成了主流。

第二，老师、家长等施教者缺乏创造力想象力，对学科的理解不够深刻没有建立知识结构（大多数就是一筐子鸡蛋的层次），而且不愿意挑战自己（有的时候还需要挑战社会，例如跟别人不一样——to be different，以及让世界因我而不同——to make a difference）。你想，如果你是一个渔夫，你是教别人钓鱼更轻松呢，还是给他两条你钓的鱼更轻松呢？而且，教钓鱼的话，还可能不成功，给鱼必定不会让他饿死。可是，问题是，如果大家都不教和不练习不探索如何钓鱼，那么，我们人类只能钓到已经钓过的鱼了。新的问题，新的方法，都不会有人去探索了。更何况我们考试的方式基本上就是在比较那个学生筐子里面的鱼更多。

第三，没有人提供如何实现理解型学习的细节的实践性的指导。我是科学家，所有的论证都需要实际的证据。所以，在我而言，不能操作和计算的东西我是不会用来表达我的思想的。因此，我在讲什么是理解型学习的时候，一定有具体的课程如何设计、一节课怎么讲、一个问题的讨论如何使用，以及整个体系的构建的例子。有理念，有例子，有体会，这才是真的落到实处。例如，“授人以渔”就必须回答什么是渔，“因材施教”就要回答什么是材有哪些材如何测量出来如何因如何教教什么。这些都没有，那么，这些就只能是口号。以系联性思考和批判性思维为基础的以学科大图景为目标的理解型学习就是渔。概念地图就是我们提出来的可以图形化体现每一个个体的思考和对学科的认识的工具。用这个工具可以实现理解型学习，可以找到每一个个体学生的具体问题，做到真正的因材施教。

第四，还有一部分人比较顽固，理念上就过不去，或者庸俗化过渡。例如当我提到数学不能以“教计算”为目标的时候，就有不少老师问，“那如果计算都不会了，其他的还怎么学？”。这是神逻辑啊。大家都知道，人活着不是为了吃饭（不否认有人或者就是为了吃饭，咱们先忽略），人吃饭是为了活着。那么，我是不是可以问，如果活着不是为了吃饭，那不吃饭活都活不了，怎么追求其他目标。是的，这个完全正确。但是，谁说过，不是目标的东西就一定要完全放弃呢？不是目标的意思是，不要单纯为了计算熟练程度而花掉这么多的时间就是来练习计算，而是要学会更高级的数学，例如把问题转化成可计算的数学问题，用数学的眼光看世界。具体如何实现这些，已经在其他的帖子里面谈到（你可以在“吴金闪的工作和思考”上搜索“中小学教育”或者“理解型学习”），就不在这里展开了。

在我们还不能改变太多如何考试，机器也没有完全淘汰人类的纯记忆性知识的时候，我们能做的事情是让自己更有想象力创造力，对学科有更深刻的认识，然后，用好理解型学习，做到“授人以渔”和“因材施教”。