分类： 教学思想和技术

今天逸儿吃早饭的时候，问了一个问题：“米”这个字怎么写？姥姥是这样回答的：先写左右两点，再写一横一竖左一撇右一捺。我不知道逸儿是不是能够把这个字通过这个书写笔画的过程想象出来，而且更进一步，就算能够想象出来，对于理解这个字有什么用。我说：逸儿，你知道木头的木吗？（回答“知道”）那就简单了，就是木头的木上面多了左右两点。它的含义就像是一个小禾苗或者小树木上面多了一点点小穗。见过长在地里的稻子吗？你知道米就是从那里来的。是不是像一个小禾苗或者小树木上面的穗子？通过这样的解释，逸儿把“米”和之前认识的字联系起来了，并且进一步通过联系生活实际，发现这样的联系还是有意义的，促进理解的。当然，实际上，按照甲骨文的字形，其本意看起来更像整个都代表的是小穗子（）。

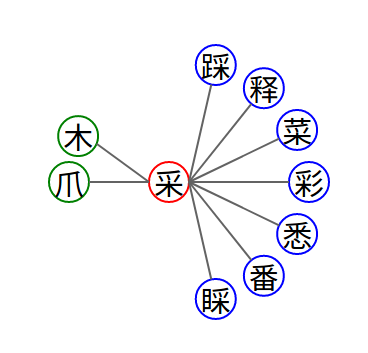
有了这个例子之后，我们还可以顺便讲讲“木”，“采”（一个手在“木”上，表示用手来采禾苗或者树木上的花果），“菜”（在“采”这个读音的基础上，加上代表草本植物的草字头），“踩”（在“采”这个读音的基础上，加上代表脚的“足”字旁，表示这个动作是用脚的做的）之间的联系。

现在，我们来对比这两个解释的方式。前者，依靠的是笔顺，确实只要孩子们记住了，字也就会写了。但是，没有任何理据性，也就是没有任何可以理解和想象的道理。后者，运用当前的字和之前认识的字之间的联系，这个字和生活的联系，这个联系和生活的联系，来帮助孩子们理解和想象，从而学会记住和运用这个字。这两种方式是完全不一样的。傻子都能够想出来哪一种方式更好了。但是，非常遗憾，前者好教啊：笔顺有标准知识库，老师可以对照着准备；后者，需要老师理解每一个字的构字理据性，有的时候甚至是古代字形，多难啊。可是，可是，你是老师啊，难道专业知识不是应该具备的吗？难道帮助学生理解世界不是教的真正目标吗？难道你的教学的目的是一堆机器吗？机器人写字可能更容易用笔顺的方式。我从小就不学笔顺——纯粹死记硬背的东西学了无益，不是照样语文学得不错，写作也能够表达自己的思想，读书也能够抓住其他人的思想。

有一个比笔顺稍微好一点的东西，叫做部首。大多数部首是有理据的，和这个字的读音或者/和含义是联系起来的。但是，很有一部分字的部首仅仅是为了查字典服务的。我们现在已经有了可以直接扫描就能够识别字的设备，为什么还要考学生仅仅用于查字典的那些部首啊。甚至，老师们还专门喜欢考这样的字，例如“开、廿、弄”三个字的部首都是“廾”。如果说“廾”的含义是两个手的话，我是看不出来“廾”和“廿”之间的联系了。例如“颖”是“麦芒”之意，所以“禾”是部首，而不是字典上所用的“页”。

因此，真正对于汉字学习有用的东西叫做“部件”，也就是那个能够把一个字和另一个字联系起来的，能够把汉字的字形和读音含义联系起来的东西。

从这里，我们发现，所谓理解，就是明白一个东西的本身的含义，然后结合这个东西的用法和这个本身的含义。理解的方式，通常是构建事物之间的联系，已知和未知的联系、内部主要结构的联系、和外部其他事物的联系。其实，这就是理解型学习在微观层面的核心：分解事物，构建内部、外部的联系，明白本来的含义。

从这个“米”字的学习上，我们还看到，实际上对于母语学习者，拼音大多数时候，是多余的。你看，孩子在生活中已经接触过“米”这个字的音和义，只需要把这个字形和音义结合起来，就完成了学习了。当然，作为辅助电脑输入、校准读音的手段，读音标注本身还是有价值的，只要内部做到自恰，没有任何固定读法，完全实现拼读。不过，这个帖子的主题不是关注拼音，就不展开了。

从这个例子往更一般化的角度来看，对于细节层面的理解型学习，我们需要首先思想上的准备：教是为了促进学，学是为了理解，理解意味着联系。其次，教的人需要对知识本身的含义以及和这些内部外部联系有非常好的把握，这个往往需要非常专业的知识和修养，以及批判性思维。再次，有的时候，通过画画概念地图，可以帮助形成西联性思考的习惯。

最后，在宏观的层面，还要能够对整个学科的大图景（典型对象、典型问题、典型思维方式、典型分析方法、和世界以及以其他学科的关系），发展方向，有好的把握，这样能够更好地决定教什么。

以小见大，用好例子，也是理解型学习的好手段。

光子的偏振状态分两种，可以用例如水平和竖直方向，45度方向和135度方向，或者任意平面内的一对相互垂直的方向，来表示。我们来看一个展示这个光子偏振状态如何描述的实验。你不需要会太多的关于光子的物理，但是，需要一个不断质疑和思考的脑袋。这个实验被称为“Dirac”的光过偏振片实验，也会出现在我的量子力学书里面。

这个实验是这样的。我们拿到如下图所示的三片偏振片，来做几个实验。

第一个，拿出来一片偏振片，对着比较明亮的地方，看看透过偏振片看世界和没有偏振片的区别。我们会发现，透过镜子看到的世界稍微暗了一点。第二个，把两片偏振片组合起来，再看看透过两片镜片能看到什么。当把两个镜片的方向（指的是里面那个方块的长边的方向）保持一致的时候，我们发现和第一个相比没变化。当两个镜片的方向相互垂直的时候，我们发现，整个变黑了，没有光通过。

这个时候，我们来猜测一次，光和镜片分别可以用什么心智模型，甚至数学模型来表示。第一种猜测，把光看作是红豆和黑豆两种豆子的组合，镜片的作用是一种镜片让红豆过去，一种镜片让黑豆过去。当只用一片镜片的时候，假设整个世界红豆和黑豆差不多多，平均起来，就是差不多一半的豆子能够透过这个镜子。这就解释了为什么一片镜子里面的世界变暗了。当用两片一样的镜片的时候，经过第一片镜子的豆子假设是红豆，则也能够经过第二片——第二片还是允许红豆过去的镜子。当两片镜子的方向垂直的时候，正好进入第一片镜子的豆子完全被第二片镜子挡住了。所以，完全没有光。这完全解释了我们到目前为止看到的现象。

或者说，其实，光子可以看做一个带了某个方向的小棒子，当棒子的方向和偏振片的方向一致的时候能通过，垂直的时候不能通过。这样的方向有两个。我们试试用这个模型来理解上面的实验现象。首先，一个镜片的时候，平均来看刚好一半的机会小棒子的方向撞上了偏振片的方向，所以变暗了，没问题。其次，两个镜片方向一致的时候，能过第一个的就能过第二个，所以现象不变，也没问题。两个镜片垂直的时候，能过第一个的就不能过第二个，完全变黑，也没问题。

如果我们的世界就这么简单，就好了。光子不过就是带着指向某个方向的一个小棒子到处飞的东西。

下面是让你的世界崩塌的一个进一步实验。我们在两个垂直的镜片中间插入一个镜片，会怎样？如果这个片子和前后两个片子中的一个一样，这个简单，之前的飞行小棒子模型就会告诉我们，没有光。这个很好，和实验结果符合。当插入的镜片是斜着的时候，我们发现，又有光了。

如果你没有觉得这个现象很神奇，我们来回到那个红豆黑豆的类比。就好像是说，第一个镜片挡住了所有的黑豆仅仅允许红豆过去，于是后面就不可能有黑豆了。可是最后的镜片仅仅让黑豆过去，因此，只要能够过来的豆子都是黑豆。这样看来，中间插入的镜片相当于把红豆变成了黑豆。怎么可能呢？镜片只不过就是一个允许某种豆子过去不允许其他豆子过去的一个东西而已。镜片不会改变豆子的颜色。

换一个例子，就好像说，第一道门挡住了所有的男人，仅仅让女人通过；最后那道门挡住所有的女人，仅仅让男人通过，现在中间加了一道门，竟然我们观察到了有人能够过这个三道门。问：中间的那道门到底如何设计？假设这个世界只有男人和女人的话。反正，我是想不出来设计方法了。

那是怎么回事？看起来，好像我们必须让中间的门能够改变光子的偏振（豆子的颜色、人的性别）才行，而且光子的偏振（豆子的颜色、人的性别）本身就允许改变。这怎么办？光子的状态怎么描述，门的作用怎么描述？

在介绍这个问题的解决方式之前，我们来看另一种状态能够改变的东西和相应的门——绳子上的波的振动方向以及烧火的钳子。下图是实验仪器。

这是实验结果：在第一张图中，右侧没有太大的振动，这个时候绳子上有两个相互垂直的钳子；在第二张图中，右侧有明显的振动，这个时候绳子上有两个相互垂直的钳子加上中间一个斜着的钳子。

这个实验说明，当中间插入一个斜着的“门”（钳子）的时候，振动可以从左边传到右边。这个实验现象和上面的偏振的现象非常像。那么，是不是理论模型也差不多呢？

我们先来看绳子上的这个现象的理论模型。首先，绳子上有振动的传播是牛顿第二定律的结果，某个方向上的一小段绳子的运动会激发附近的绳子的同样的方向上的运动——在这里这个运动是垂直于传播方向上的平面内某个方向上的振动，而不是真的在随着波传播的方向在运动。每一小段绳子不传播这一点，加上，整个运动的理论模型是矢量形式的牛顿定律这一点，是非常关键的。在这样的模型下，我们来看这个三道门的实验现象的理解。

首先，当只有两道相互垂直的门的时候，右边没有振动。振动先传到第一个门，由于其在水平方向上，因此只有水平方向的振动可以传过去。接着这个水平方向的振动传播到了第二道门。这个门在竖直方向上，仅仅允许竖直方向上的振动传过去。但是，传到这道门的水平方向的振动没有竖直方向的分量，于是，右侧不会有振动。好。

接着，当中间加上一道门之后，过了第一道门来到中间的门的振动是水平的。中间这道门是斜着的，不是水平，不是竖直。于是，水平方向的振动有斜着的分量，会把斜着的振动传播到中间的门的右侧。过了中间的门，来到了最右边的门——竖直方向。这个时候，斜着的振动，具有竖直方向的分量，于是，能够把竖直方向的振动传到右边。

整个过程的基础，或者说数学形式，就是，来自于矢量形式的牛顿第二定律的矢量分解，或者说代表振动方向的矢量和代表门的方向的矢量之间的内积——只要内积不为零，则存在分量，能够传过这个门。

好了，我们来看，这样的矢量和矢量内积的数学是不是也能够描述光子过三个偏振片的实验，更进一步，是不是其基础也是牛顿第二定律。注意，牛顿第二定律的基础是绳子上每一小段之间的拉拉扯扯的相互作用。而在光子的情况，光子不是介质波，本身可以在真空中传播，没有背后拉拉扯扯的东西在。因此，其机制肯定就不是矢量形式的力的相互作用和相应的牛顿第二定律。那到底是什么？

我们也已经看到，这个代表振动方向和门的方向的矢量，以及两者之间的矢量内积的数学形式，能够解释这个实验现象。问题仅仅在于这个矢量数学的背后不能是牛顿定律。那么，是什么？

关于是什么，我就不讲了。我们仅仅需要知道，这个光过三个偏振片的实验使得我们认识到，需要用矢量来描述偏振方向和偏振片，两者之间还需要做内积，并且其基础不是经典力学的牛顿运动定律就够了。

除了知识上的目标，以及用来说明为什么量子力学的数学形式会这样，我还想用这个例子了来说明——哦，这个也任务交给读者。记得去使用WHWM，问传达什么信息，如何传达，为什么这个信息，为什么这样传达，对我有意义的我喜欢吗，这几个问题。同时也可以去看前一个帖子“能看到光是多么神奇的事情啊”的总结。

上课做了一个实验之后，学生说：这个实验以及您提出来的问题迫使我们做深入的批判性的思考，但是，从这个思考的结果看起来，我们之前对于光过一片玻璃，而不仅仅是这个实验中为了展示神奇之处用的三篇玻璃，的理解，也是有问题的啊，因为一个好的理解应该能够解释所有的这些现象啊。是的，说得很好。这个例子也会找时间写出来。今天我再举一个光过玻璃的例子。这个例子来自于Feynman的《光和物质的奇异性》。

大家都见过相机镜头。你会发现一般来说镜头是有颜色的。这个颜色来自于镀膜——给相机玻璃上增加一层其他材料。其主要目的是增加透光率。有的时候是所有颜色的光的透光率，有的时候是为了增加某些颜色的光的透光率。现在，问题来了，为什么增加了一层膜之后，会增加透光率呢？

按照我们日常的体验，或者中学学过的光的反射和透射，我们知道每增加一个界面光就会发生反射。于是，我们粗糙地假设每一个界面\(4\%\)的光会被反射走。那么，能够通过第一个界面的光就是\(96\%\)。接着，这个\(96\%\)的光会通过下一个界面，继续发生反射，大约又会有\(4\%\)的光被反射走。于是，经过一个玻璃或者膜的两面之后，通过率会差不多等于\(92\%\)。按照这个图景，增加的膜越多，则透过的光越少：你看，就像一个小球打过来，每次都要反射走一部分啊。或者说，这个图景实际上是把光看做一个个服从概率理论（具体指的是独立事件的乘法——如果一件事情有前后两件独立的事情组成则这件事情的概率是那两件事情的概率的乘法，和互斥事件的加法——如果一件事情有两种完全排斥的可能发生的方式则这件事情的概率等于这两个方式的概率相加）的小球。这样的服从概率论的经典小球的模型你是深有体会的。那么，这样的模型能不能用来理解光过玻璃呢？不行。如果这样的话，通过镀膜增加界面是不可能增加透光率的。那怎么办？

为了更清楚地展示这个模型的困境，我们来看如果一个一个小球打过来，会怎样。任何时刻，我们保证整个空间只有一个小球。这是做得到的，通过使用一个叫做单光子光源的仪器。现在，我们来看这一个小球。先到达第一个界面，假设被弹走了，故事结束。这个可能性是\(4\%\)。假设透过了第一个界面（这个可能是\(96\%\)），现在来看这个小球到达第二个界面时候的情况。这个时候还是有两种可能，透过了，故事结束。这个可能是\(96\%\times 96\%\approx 92\%\)。如果弹走了（这个可能是\(96\%\times 4\%\)），则故事差不多结束。这里“差不多”的含义是实际上，我们还应该考虑多次的反射。不过为了简单性计，就不再计算了。

经典波动光学是这样来解释的：把一束光看作是好多好多小球合起来构成的，或者是介质上的振动形成的。我们先来看好多好多小球合起来的视角。说，到达一个界面的时候，我们把小球们分做两部分，一部分弹走，一部分进入玻璃。对于进入玻璃的那一部分，在第二个界面还是会分成两份，一部分透过整个玻璃，一部分回弹到第一个界面。对于回弹到第一个界面的那部分，其中的大多数小球会透过第一个界面出去，和那些第一次就被弹走的小球们合在一起。当合在一起的时候，不知道什么样的原因，这两部分小球就会有相互干扰，例如相消，于是，整体反射光减少。所以，能够只能通过透射光出去，于是透光率增加了。在这里，神奇的地方就在于：你如何让两束光里面的小球们相互影响？光的这些小球们很独立的，基本上不发生相互作用。因此，这个很多个小球的模型不是一个好的模型。

再来看介质上的振动的视角。介质上的点的振动之间确实时会发生影响的：一个点的振动会带动附近的其他点的振动，并且如果有两个振动源的效果传到了同一个点上，则这个点的振动应该是传过来的两个效果的矢量叠加。为什么是矢量叠加？因为这两个点的振动传播过来的方式符合牛顿第二定律，而这个定律是矢量形式的：哪个方向上有里的作用则那个方向上产生运动的改变。这样来看，我们可以很好地理解前面的这个透光率增加的事情。实际上，这个现象有一个名字，叫做光的干涉。具体来说，是这样的。一束光在第一个界面分开成两束，反射和投射。反射的光就好像是从界面上的反射点开始的一个往玻璃外面的空间传播的介质波。透射光呢就是往玻璃内部传播的介质波。接着，透射光遇到第二个界面。这个时候，再次分成两束。第二次投射的那部分不用管了，故事结束。在第二个界面上发生反射的那部分的那部分光就会回到第一个界面，而且其中的大部分会透射到玻璃外面，和第一次反射的光可能会到达同一个地点。这个时候，在这个同一个目的地上，就会发生来自于牛顿第二定律的矢量叠加，于是，发生相消（或者相长）的事情。可是，这个解释有一个很大的问题，光子不是介质波，其背后没有牛顿第二定律，没有矢量性。怎么办？

我们已经看到了，经典单个小球的模型不能解释增加透过率这个事情，经典多小球模型也不行，经典介质波模型也不行。我们再来看看量子力学又怎么解释这件事情。

量子力学是这样来解释这个问题的。还是假设我们每次在整个空间中只有一份光的能量，称为光子。量子力学问，光子反射回去这件事情有集中发生的可能啊？第一种，第一个界面就发生反射。第二种先在第一个界面发生透射，然后在第二个界面发生反射，接着回到第一个界面发生透射。无脑量子力学说，凡是这样的一件事情有两种“不可区分”（大概来说就是问，如果你在玻璃的第一个界面的外面观测到一个光子，你能够知道是第一种还是第二种方式来的吗？不能就是不可区分。实际上，精确含义更加复杂）的方式发生，则需要把这两种方式（的概率幅，而不是概率）做直接相加。这个时候，你只需要算一个相加得到的概率幅对应的概率，自然就得到既可以相消也可以相长的结果。

但是，你仔细想，这个事情还是很神奇啊，还是有问题啊。你看，只有一个光子的情况下，第一个界面就反射走的光子，有怎么会“遇到”并且“影响”，那个先透射再反射再透射的光子呢？整个空间只有一个光子啊！于是，只要第一次被反射走了，那么，后面的事情就不可能发生了，那怎么相互影响相互遇到啊！如果说，第一次没有被反射走，则整个空间的唯一的光子也就只会发生后面的两种可能啊，不可能再和那个从来没发生过的第一次就被反射的光子来相互影响啊！怎么办？

然而，量子力学的神奇之处就在这里：只要一件事情有两种发生的可能，这两种可能还不可区分，则整个事情的概率幅等于两种方式的概率幅相加，接着概率相当于概率幅的绝对值的平方。通过这个先相加后做绝对值的平方，我们就能够得到和经典介质波数学上一样的矢量叠加的形式。

下面的公式就表示了这个意思，尽管根本没希望读者们真的看懂：
\begin{align}
\rho^{c} = p_{1} \left|1\right\rangle\left\langle 1\right| + p_{2} \left|2\right\rangle\left\langle 2\right| \\
\rho^{q} = \left(\sqrt{p_{1}} \left|1\right\rangle + \sqrt{p_{2}} \left|2\right\rangle\right)\left(\sqrt{p_{1}} \left\langle 1\right| + \sqrt{p_{2}} \left\langle 2\right|\right) \\
= p_{1} \left|1\right\rangle\left\langle 1\right| + p_{2} \left|2\right\rangle\left\langle 2\right| + \sqrt{p_{1}p_{2}}\left(\left|1\right\rangle\left\langle 2\right| + \left|2\right\rangle\left\langle 1\right|\right)
\end{align}
前者表示\(1,2\)两种方式按照各自的经典概率\(p_{1},p_{2}\)来相加，后者表示这两种方式按照其概率幅（大约可以看做其开平方\(\sqrt{p_{1}},\sqrt{p_{2}}\)）来相加，然后再求其绝对值平方。这样就会多出来最后那个括号里面的额外的项，而它们就是那些导致相消或者相长的部分。

通过这个例子，我想体现——哦，这个任务交给读者。记得去使用WHWM，问传达什么信息，如何传达，为什么这个信息，为什么这样传达，对我有意义的我喜欢吗，这几个问题。同时也可以去看前一个帖子“能看到光是多么神奇的事情啊”的总结。

今天上课，讲了无介质波的叠加原理——z方向向上态和z方向向下态可以加起来变成x方向向上态，或者说x偏振和y偏振可以加起来变成某个角度的偏振光，而不是一会儿x一会儿y偏振的组合。忽然想起来，其实，我们能够看到光，这件事情是多么的神奇啊。例如，Einstein就曾经特别想不通这件事情。

白炽灯的光，我们天天见，从来不觉得神奇。连多想一下都不会去想，如何神奇呢？待我慢慢道来，来挑战你的思考。

先看水面的波：扔一个石头（假设石头特别小，看做一个点），水波沿着水面扩散。如果在某个地方有一个观测者——例如一个浮漂，则过一段时间，水波传播到了那个地方，浮漂就会动，也就是观测者看到和水波。这个时候，基本上可以预测，沿着某个圆圈（石头入水处为中心经过这个浮漂的一个圆）的其他地方都可以观测到水波。这个水波很好理解——很好理解可以解释为原则上可以通过牛顿定律来计算。

再来看灯泡发出来的不神奇的光：假设灯丝特别小，看做一个点，则我们会看到和水波一样的事情——当某个地方的观测者看到光的时候，我们可以推测，同样大圆（这时候是大球）的地方的其他观测者也会看到光。当然，由于光的传播速度很快，有可能我们的日常生活体验会告诉我们说，只要一个地方有光任何地方都会有光。

为了解决这个问题，我们需要做两件事情：走的比较远，以及让灯丝每个时间段里面仅仅发出一个光的能量单元，或者一个批次的光的能量单元。这样的一个实验装置是有的，而且这样做好像很无辜啊，没什么特殊之处。现在，我们沿着这个无辜的思路来看看特殊之处。

在这个对于把光看做是水波的第一阶段的认识，我们发现，实际上，我们是把光相当于看做是通过某种介质往外传播的东西。这样，我们就有了一个光和光的传播的心智模型——介质上的振动，和水波类似，只不过沿球面向外传播。这个看起来好像很有道理，也一点都不奇怪。

当然，实际上，我们知道光的传播不需要介质，也不可能有介质。这个需要做个实验来证实，例如第一个让光在真空中传播一下，第二个做一下著名的迈克尔逊-莫雷实验。我们在这里就先承认光的传播不需要介质。这时候，我们再来看，白炽灯的灯光在某处被一只眼睛接收到这件事情。

那先这样看：试试豌豆射手射向四面八方的豆子的模型。灯泡光发出来的光，可以看做是由去往四面八方的一个个光子构成的一群光子合起来的效果。针对这个模型，眼睛能够接收到光也一点都不奇怪，就好像有一个圆形的弹幕，其上任何一点都可能接收到豌豆射手射出来的豌豆。为了看到这样的一个解释的不足，我们来调整一下光源——让光源在任何一个时刻只能射出去一个光的能量单位（称为光子），就好像豌豆射手在任意一个时刻（中间可以特意做成某个时间的间隔）仅仅射出去一个豌豆一样。这样的单光子光源的调整真的是实验上能够做到的。如果要让现象差不多一样，则需要豌豆或者光子的出射方向是某种意义上的随机的方向。

这个时候的随机有两种形式：一种是，任意一个时刻出射的光子都可能向着任意的一个方向，也就是一个所有的方向都具有同样大小的概率密度的概率分布函数；另一种是，任意一个方向上都具有概率密度幅的，整体上表现为所有的这样的概率密度幅加起来的某种分布函数（量子力学的语言，称这样的密度幅的“分布函数”为密度矩阵）。大概来说，相当于
\begin{align}
\rho^{c} = \frac{1}{Z}\int d\Omega \left|\theta, \phi\rangle\langle \theta, \phi\right| \\
\rho^{q} = \frac{1}{Z}\left(\int d\Omega \left|\theta, \phi\right\rangle\right)\left(\int d\Omega \left\langle \theta, \phi\right|\right)
\end{align}
这些公式都是示意公式，仅仅表示前者是概率相加，后者是概率幅相加的意思。现在，我们来看这两种解释哪一种比较有道理，如果我们用它们来理解眼睛看到光的时候的光的状态这件事情。

我们先来看第一种——概率组合。首先，某个方向上的眼睛能够看到光这件事情在这个模型下，很好理解：正好那个随机的光子跑向了那边，于是就刚好被探测到了。这个时候，在这个时间间隔内，其他任何地方都不会探测到光子。注意，在这里，由于经典随机性的存在——例如当我们观测一个随机的硬币发现是正面的时候，就是因为刚好看到了正面，我们不用去担心那反面的几率上哪里去了，怎么会消失了的这件事情——我们不需要担心其他地方的光子跑到哪里去了的问题：那些地方仅仅是有光子到达的可能，而不是真的有光子跑到了那些方向去了，然后由于某个方向上实际探测到光子，这些其他方向的光子又需要从其他方向消失，或者说相当于“塌缩”到正好被观测到的方向的问题。

注意，这个时候，回到水波的模型。如果水波上，我们也看到了类似的现象——一个石头扔进去以后，在某个方向发现了水波，但是其他任何方向没有水波——则，肯定需要问上面那个问题：其他方向的水波难道就真的“塌缩”到了刚好被观测到的方向吗？因此，我们就发现，由于有这个物质波而非介质波的效果——能够控制一个个光子来传播，而不需要介质来产生振动来传播，实际上，介质波的理解是有问题的：真的需要解决瞬间“塌缩”如何发生的问题。所以，初始的用水波来当做光波的心智模型的尝试是不对的。

上面已经提到了，把介质波改成概率波，可以解决这个瞬间“塌缩”的问题。那么，是不是概率波就是对的呢？这个需要做一个叫做双缝干涉或者Which-way实验来证明概率波模型也是错的。如果是概率波，假设我们仅仅取整个空间中的两个方向来做实验——在这两个方向上各自开一个缝，其他的方向上都挡住。先测量仅仅打开一个缝的情况，得到一个经过这个缝到达屏幕的一个实验结果——一个光子达到屏幕的分布函数。这样得到两个分布函数。然后，在考虑概率叠加原理，当一个事情有两种互斥的方式发生的时候，整体的结果等于两个结果的概率相加，于是，我们就得到了打开两个缝的实验结果——应该是分别打开的情况下的概率相加。然而，实验结果发现，不是概率相加，同时具有相长和相消的效果。相消的效果是不能够用概率相加来解释的，如果一定的概率妈妈给孩子五块钱，一定的概率爸爸给孩子十块钱，则平均来看孩子的钱肯定在五块到十块之间。但是，量子的实验告诉我们，有可能得到两块钱，或者二十块钱。这个仅仅在做矢量叠加的时候才有可能，在概率相加的时候是不可能的。

这样，我们就被逼又回到了光子的各个方向概率幅相加的心智模型。可是，这个模型的数学形式和介质上的波很像——在那里，振动方向可以做矢量叠加，于是也就会出现不在五块到十块之间的情况。

问题又来了，如果确实像介质波，那么，我们就又要问，如何来理解瞬间“塌缩”的问题：在某个方向上看到光子之后，整个空间就没有其他光子了，这个看起来，相当于，把观测值钱的其他各个方向上都具有探测到光子的可能性，全部都“塌缩”到了观测到光子的那个方向了。如果确实是这样，将会是大问题：我们可以离光源很远很远，几百万光年，于是，其他方向的光子完全不可能用任何方式传播或者说“塌缩”到观测到光子的方向上去。这怎么办？

其实，这还是用了介质波来理解概率幅波。几率幅波真的没有表示有真的光子传过去的意思，因此，也就不需要在探测到光子的那个时刻，把其他方向上的光子传回来的这个步骤。如果是介质波，就需要这一步。因此，在介质波上也就看不到这样的现象：仅在某个方向上探测的光子，其他方向完全没有探测到光子。

在这个思考中，针对不同情况的实验结果，我们尝试了光的介质波模型、概率波模型、几率幅波模型的介质波理解、几率幅波的几率幅理解。我们发现，只有后者能够解释眼睛看到光这件看起来如此简单的事情。当然，我们还有一个隐藏的要求：不管哪个光子的实验，其结果，都可以用统一的理论来计算和理解。

通过这个例子，在知识上，我希望能够促进对几率幅波的理解，能够促进对什么是科学以及科学和数学的关系的理解——科学就是一个系统化的能够得到和实验现象相符的可计算分析的心智模型的集合；在思维方式上，能够学会不断地层层递进地做批判性思维和对比性系联性思考。同时，我也想通过这个例子说明：学习就是学会一双眼睛，从平凡中看到神奇，从神奇中复又看到平凡或者平凡和神奇的共存。学习是为了理解世界。

今天早上，心儿问我一个问题：爸爸，基因有几种，每个人的基因都不一样吗？我不知道具体心儿问这个问题的缘起是什么，但是这是一个很好的问题。考虑到每个人的基因大约确实不一样，并且不同的基因只有四种，这是一个有意思的问题：确实只有四种，每一个地方可以放四种之一，但是架不住有很多的这样的地方啊，于是一排列组合就很多。为了给心儿体验一下这个排列组合问题，我说：我去查查人类基因总共多少种，但是我知道基本的基因只有四种，人类有很多，而且差不多每个人都不一样，尽管亲人之间相似的地方多一些；这个四种和很多种的关系可以考虑下面的问题来体验一下——一个盒子里面可以放一颗红豆或者黑豆，有几种不同的放法；两个盒子的每一个可以放一颗红豆或者黑豆，有几种不同的放法；三个盒子呢？

大约是这个“几种放法”的说法没听懂，孩子就瞎蒙了几个答案，一个盒子两种，两个盒子四种，三个盒子六种。这时候我注意到我的问题没出好（换成三种豆子就更好了），导致前两个答案不反映背后的思考。尝试了一下换一种表达，还是没明白，孩子就去上学去了。放学回来以后，我拿出来一堆豆子，几个盒子。让心儿先玩。玩了以后画图，记录下来每一种放的方法。玩到三个盒子的时候发现了规律，四个盒子的时候验证了规律。我问：那到底规律是什么，为什么？心儿回答，每多一个盒子乘以2（我还是没有改题目，其实应该改成三种豆子的），至于为什么说不清楚。我就让心儿继续玩，继续对比她画出来的图，直到最后搞清楚那个为什么。她说的那个为什么过程比较多，这里，我给出来我的。当然，说清楚为什么有很多种不同的方法，每一种背后的思维都不一样。其中一种可以是这样的：每增加一个盒子，这个盒子里面可以放红豆或者黑豆；当是红豆的时候，前面已经有的盒子的放法不会被改变，因此就有了之前那么多种；同样的当是黑豆的时候，也有之前的那么多种；因此，合起来就是两个前面的那么多种。注意这里我没有用乘法，用的是加法，甚至仅仅是加法的精神。

对于一个学过排列组合的人来说，可能下面的理由是过得去的：每一个盒子有两种放的方式，因此，所有的\(N\)个盒子合起来就是\(2^{N}\)中放法。对于解决这个问题本身来说，这个答案更快，更不容易出错。挺好。但是，从获取面对现象、提出问题和解决问题的经验来说，前面那个“提出问题、玩（或者两个顺序倒过来）、猜测、检验、思考为什么”的过程好很多。排列组合不用教，只要明白是什么，为什么，自然就会了。那，其实，所有的知识都应该这样来学习：不教而教。这就是我在“信息时代教什么怎么教？”还有“机器人能够取得高考好成绩意味着什么？”里面提到的，教什么怎么教的例子。

只要有心，一个日常生活的例子，或者一个教材中需要教的知识，也可以变成一个可以体验的，可以让学生从中获得提出和解决问题经验的，体验深入思考为什么的问题。在这个细节处理的基础上，这个时候，再加上对整个学科的理解和内容选择，也就是围绕学科大图景——典型对象、典型问题、典型思维方式、典型分析方法、和其他学科以及世界的关系——来选择教什么，就可以实现“教的更少，学得更多”，就可以做到学会学习和思考，学会和喜欢创造。

很多很多时候，当掌握一个学科的大图景之后，学习新概念新知识，只需要从一个问题或者一个实验开始就够了，其他的，只要明白了，自己就能独立地，或者在老师的少量帮助下，构建起来。当然，选择哪些知识来构造，还要靠老师的设计。