分类： 中小学教学

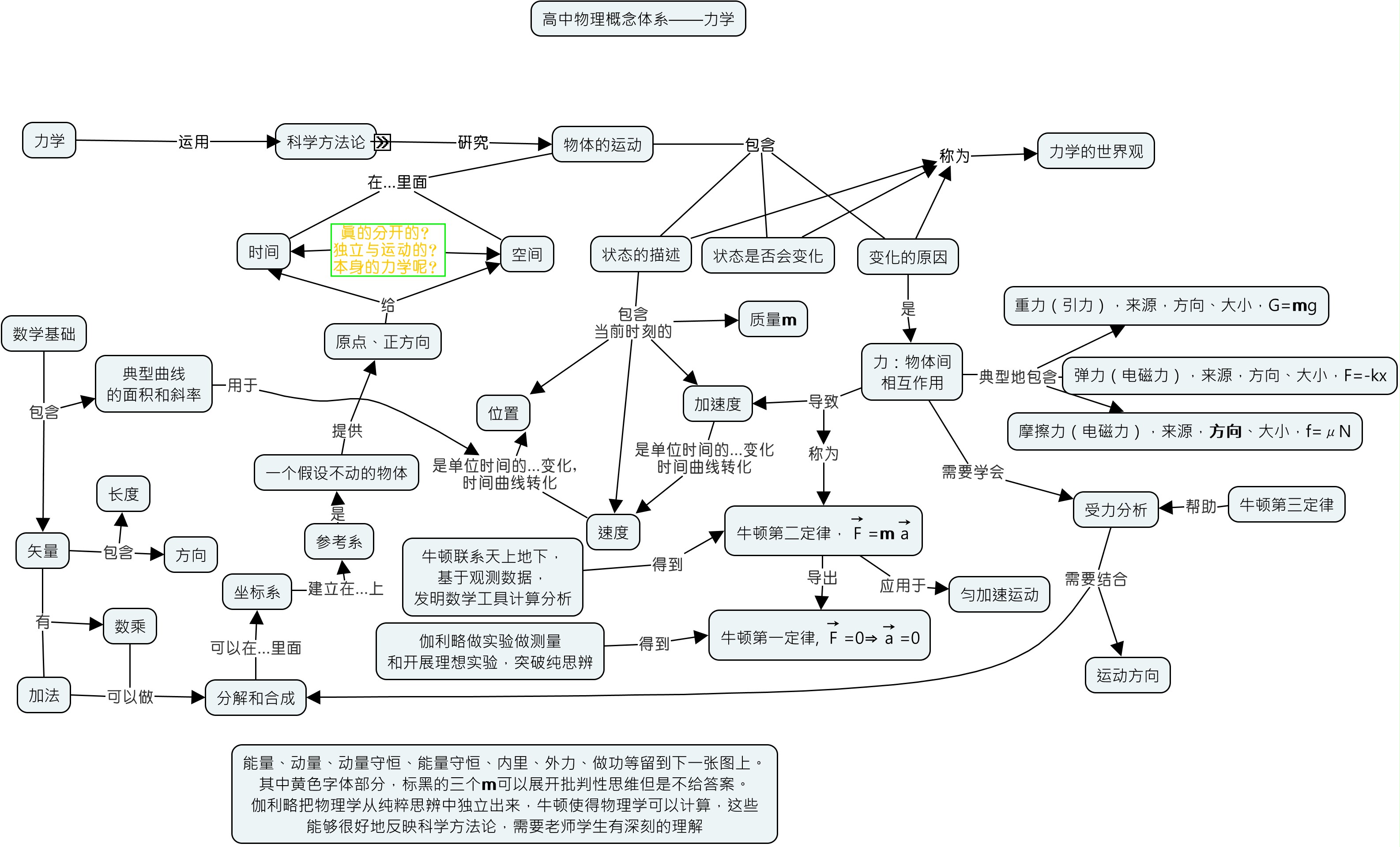
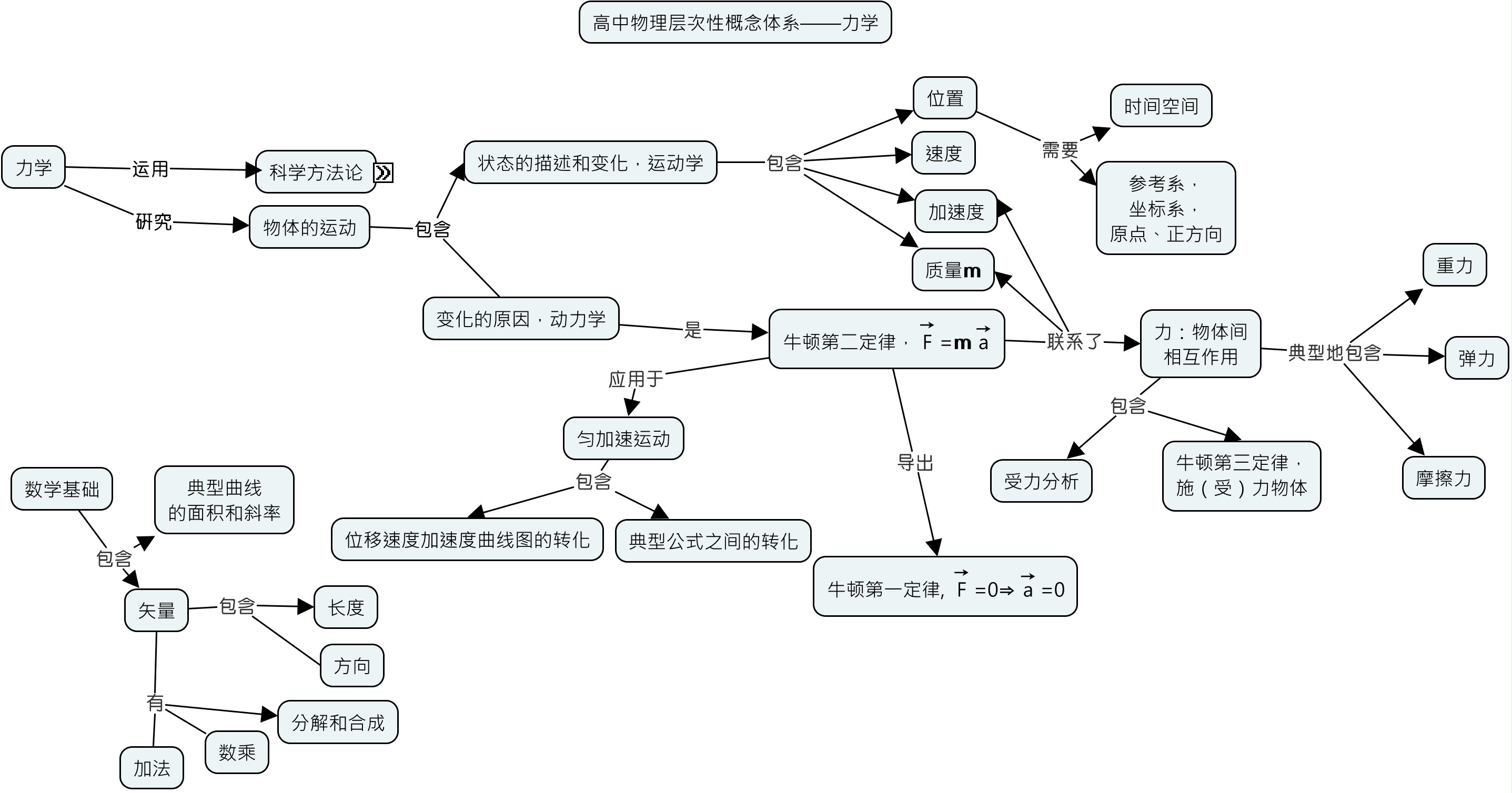
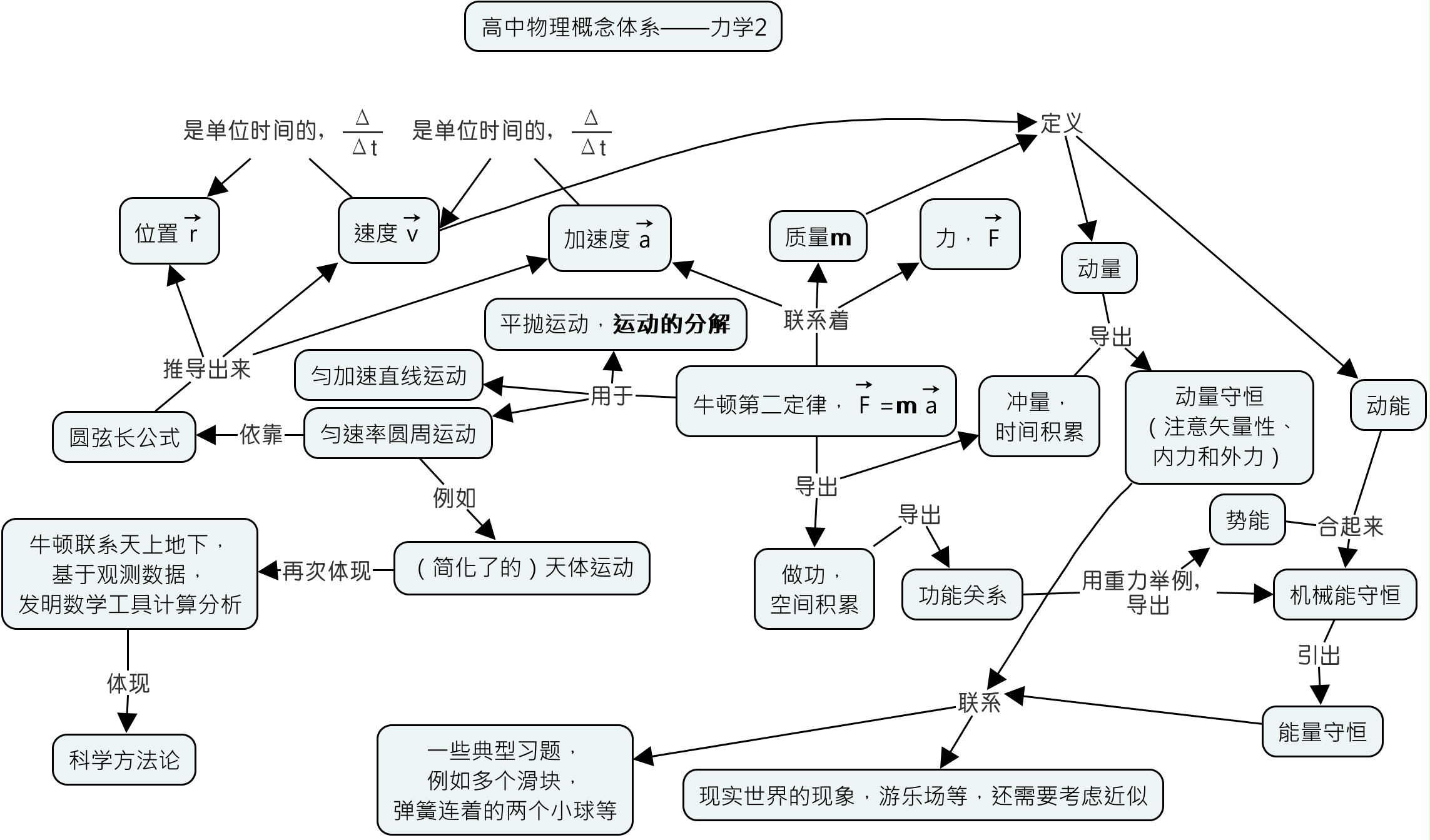
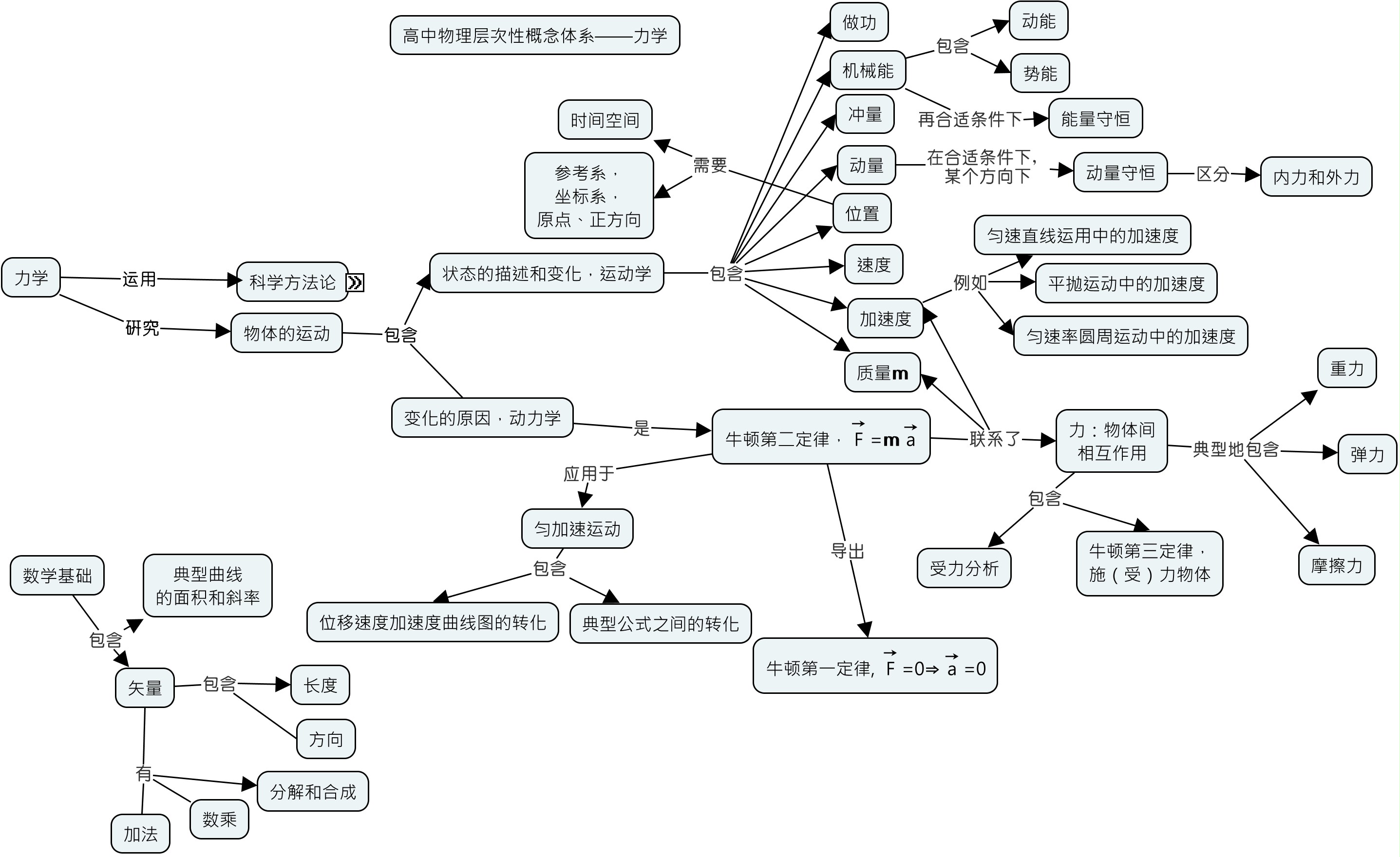
退括号的机械式学习和理解型学习提到有一些规则是要依靠做题的熟练和记住的。这是典型的机械式学习。其中，我们也提到，就算是这样的规则的学习，学习的方式也主要就是重复，我们也可以让理解型学习发挥作用：用来明白这些规则为什么是这样的，也就是大概形成对这些规则的一定程度的理解，然后再来通过题海战术达到记住和熟练。

但是，今天，我发现，这个还不够，理解型学习，还可以用在计算的过程中。这样才能真的做到事半功倍，通过做少量的题来达到熟练和记住的目的。怎么发挥作用？在计算的任何一个步骤过程中，思考，这一步是按照什么原理或者规则来做的，也就是追问“每一步算出来的结果是什么”和“为什么能够和需要这样计算”的问题。

例如这样的一道面积计算题：一个大长方形里面挖掉一个小长方形，求剩下的部分的面积。挖掉的长方形长度是56cm，宽未知。大长方形的宽为44cm，长未知。剩下的部分的就是一个L形长条，其长条宽度为13cm。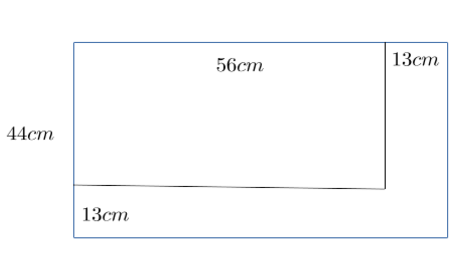

如果用大长方形减去小长方形（这一步思考我认为是这个问题最关键的，但是…），则
\begin{align}
\left(56+13\right)\times 44 – 56\times\left(44-13\right)
\end{align}
我家心儿是列出来的算式是这样的
\begin{align}
\left(56+13\right)\times 44 \times 56\times\left(44-13\right)
\end{align}
问第一个括号里面是什么，明白是大的长度，最后的那个括号是什么，明白是小的宽度。问，第一个乘积符号是什么意思？算面积？问最后那个乘积符号是什么意思？算面积。问中间那个乘积符号是什么意思？面积乘以面积是什么？不知道，意识到把周长和面积搞混了。还不是简单地搞混，各自是清楚地，不知道为什么放在一起就能搞糊涂。不过这个不是重点，重点是，通过问每一步计算出来的是什么，就可以自己找到问题，并解决。

也可以把剩下的形状拆成两个长方形（或者等价地，这一步思考我认为是这个问题最关键的，但是…），
\begin{align}
13\times\left(56+13\right)+\left(44-13\right)\times 13
\end{align}

接着就可以开始做计算了，计算部分纯粹就是规则的运用，我以为没什么。但是，你看，心儿会这样算（在这个问题中到还真的没有错，算对了。我实际上是把下一个问题中心儿犯的错移到了这里。道理上是一模一样的），
\begin{align}
13\times\left(56+13\right)= 13\times 56 \times 13
\end{align}
或者
\begin{align}
13\times\left(56+13\right)=13\times 56\times 13\times 13
\end{align}
看起来好像就是分配律记错了，改了就完了。实际上，当然也是，但是不仅仅是这样。分配律错了仅仅是表现，根本问题在于没有仔细问每一步为什么这样算。为什么这样说？首先，心儿算过不少尽管也不多分配律的问题，确实都算对了。其次，看得出来，她心里不太愿意算或者什么原因，就想着完成这道题了。我演示了这样的一个计算。
\begin{align}
13\times\left(56+13\right)+\left(44-13\right)\times 13 \\
=13\times 56 + 13\times 13+44\times 13 -13 \times 13 （乘法对加法的分配律） \\
=13\times 56 +44\times 13 + 13\times 13　-13 \times 13 （加法交换律） \\
=\left(13\times 56 +44\times 13\right) + \left(13\times 13　-13 \times 13\right) （加减法结合律） \\
=\left(13\times 56 +44\times 13\right) （算出来最后的减法） \\
=\left(56\times 13 +44\times 13\right) （乘法交换律） \\
=\left(56+44\right)\times 13 （乘法对加法的分配律） \\
=100\times 13 （算出来加法） \\
=1300　（算出来乘法）
\end{align}
也就是在每一步的等式的后面标注等式成立的理由是什么。
然后，问，你的计算的每一步的理由是什么，心儿就能够自己找出来问题在哪里了。

通过这个例子，我想告诉大家，就算在熟练和记住规则这样的几乎完全就是机械式学习的任务上，理解型学习也是可以发挥作用的。其发挥作用的方式就是在计算的每一步问：“算出来的是什么”，“为什么能够和需要这样来计算”。更一般地来说，语文数学英语都一样，其实什么都一样，不过就是多问几个问题，问是什么，问为什么，问WHWM。

当然，我再一次强调，理解型学习的真正威力不在这里，而在于使用概念地图帮助理解型学习的四个层次。

又多了一道题的例子：小林和小文各自有200元钱。小军从每人那里借了25.5元。这时候三个人的钱一样多。问小军原来多少钱？

心儿列出来算式是这样的\(\left(200-25.5\right)-2\times 25.2\)。这个很对。但是，我接着问：\(\left(200-25.5\right)\)是什么？答小林和小文的钱。问他们什么时候的钱？答借走以后剩下的钱。问\(2\times 25.2\)是什么？小军借到的钱。\(\left(200-25.5\right)-2\times 25.2\)合起来是什么？小军原来的钱。为什么？小林和小文的剩下的钱减去小军借到的钱，为什么会是小军原来的钱？不知道。可见，还是没有学会思考“是什么”、“为什么”，至少没有学会主动去问这些问题。中间最关键的一步就是由于“这时候三个人的钱一样多”，因此，从数值上，\(\left(200-25.5\right)\)也是小军最后的总钱数。于是，才有小军的总钱数减去小军借到的钱，等于小军自己原来的钱的数目。

在这里例子里面，每一步计算出来的是什么，分别是“小林和小文的剩下的钱（同时也就是小军最后的总钱数）”、“小军借到的钱”还有“小军原来的钱数”。为什么需要这样算，是因为需要计算的是“小军”的原来的钱，已知的是“小军”借到的钱，因此，前面也必须是“小军”的钱。为什么能够这样算，是因为“这时候三个人的钱一样多”，数量上小林和小文的剩下的钱等于小军最后的钱。希望通过这个例子能够更好地学会问是什么为什么，更好地做严密的思考，每一步都有理由的思考，于是达到事半功倍。

顺便，心儿，错了不要紧，关键是要从错的地方学到东西，而且有的时候要追问更深层次的原因在哪里，而不满足于算错了，看错了，也不满足于改过来了。例如，在这里，学会了问“算出来的是什么”，“为什么能够和需要这样来计算”之后，就能够自己发现错误，自己改正，自己提高了。这样做提道题的效果就相当于不思考是什么和为什么的时候的算100道题的效果。

阅读理解题：这个帖子主要说了什么信息（What），用什么例子采用什么逻辑怎么来（How）说明的这个信息，为什么（Why）作者要说这个以及用这样的例子和逻辑来说，你读了以后有什么感想和思考对你意味着（Meaningful）什么。

今天心儿做一些计算题，需要用到退括号和加括号。当然，从训练计算熟练程度的角度来说，这样的计算题没有意义。反正心儿都是不管三七二十一用竖式计算的，尽管慢点，但是，答案是基本正确的。换一个角度，学会从观察事物然后发现事物的规律，凑某种特殊构造的角度来说，简便计算题还是有一定的训练意义的。

退括号有很多的类型。要记住所有的类型是一件很不容易的事情。例如，

1. 括号外面是加号的，里面是加减号的，展开以后里面的算符不变。
2. 括号外面是减号的，里面是加减号的，展开以后里面的算符变号。
3. 括号外面是加减号的，里面是乘除号的，展开以后里面的算符变号，但是先算乘除后加减。
4. 括号外面是乘号的，里面是乘除号的，展开以后里面的算符不变。
5. 括号外面是除号的，里面是乘除号的，展开以后里面的算符变号。
6. 括号外面是乘号的，里面是加减号的，展开以后里面的算符不变，乘号要用分配率乘到每一个上去。
7. 括号右边是除号的，里面是加减号的，展开以后里面的算符不变，除号要用分配率除到每一个上去。
8. 括号左边是除号的，里面是加减号的，没法打开括号。

你看，随便写写就有这么多条。当然，通过大量的计算练习，这些规则都是可以记住的，甚至可以专门来背。这就是典型的机械式学习：学习的目标是学会规则，学习的手段是重复练习。

现在，再来看理解型学习在这里怎么用。第一，这种规则的学习本身不是理解型学习的强项（以概念地图为基础的理解型学习的真正强项在于：第一，整理知识结构，梳理事物之间的联系，并且依靠这些结构来选择教什么，学什么，考什么，怎么教，怎么学，怎么考；第二，用好WHWM问题促进阅读、表达和思考。）。第二，还是可以做到事半功倍的。例如，对于第一条的理解：你想，你本来是类似这样的\(80+(20+3)\)，需要去括号，也就是变成\(80+20\pm 3\)这样的，咱们需要决定其中的\(\pm\)到底是什么；这时候，你就考虑有括号的那个\(80+(20+3)\)比没有括号但是只有前两项的\(80+20\)大还是小？肯定大，因为后面的那部分被先加起来了。于是我们知道最后的是加号。例如，对于第二条，\(80-(20+3)\)，去掉括号，就大概成了\(80-20\pm 3\)；接着想，你就考虑有括号的那个\(80-(20+3)\)比没有括号但是只有前两项的\(80-20\)大还是小？小，因为减去的是两者合起来，现在仅仅减去其中一项，于是还得再减，所以最后的是减号。

同样的道理，可以理解乘法的分配率。例如\(10\times (20+3)\)可以看做每本书10元，先买了20本，接着再买了3本，问总共多少钱。自然地其中一种计算就是先算出来书的总数，接着计算总钱数，也就是\(10\times (20+3)\)，或者可以先计算买20本书的钱，再计算买3本书的钱，于是就有\(10\times 20+10\times 3\)。两者应该相同。于是，就得到了乘法分配率。

当然，就算这样理解之后，还是需要通过大量的计算才能熟练。但是，至少，就不再依赖于纯粹记忆了，而是明白了再记。当然，对于这种学习目标本来就是规则的，一定量的练习还是需要的。好处就是，有了这样的理解再去记忆，有可能不用做这么多的题，就可以运用自如了。因此，就算用题海战术，概念梳理，题目梳理，也是很有意义很有帮助的。

为了实现“教的更少，学得更多”，“学习更少，学到更多”，我提出了基于概念地图和理解型学习的“大图景”教学体系。现在，我来试着把高中物理的这样的体系整理出来。

大图景是指这个学科的典型研究对象和问题、典型思维方式、典型分析方法、典型应用（和现实还有其他学科的关系）。理解型学习的意思是要运用好系联性思考和批判性思维，通过把事情搞明白来学习。系联性思考就是把一个东西放到和其他东西相互联系的角度来理解这个东西，同时尽量使得所有的东西都通过这样的方式相互联系起来，达到用更少的线索和基础概念把更多的概念整合起来的整体结构。批判性思维的意思就是在你自己想清楚为什么之前不要接受任何的结论或者论证过程，一定要不断地问为什么；同时，问这些为什么的时候，要结合系联性思考，争取给自己对这个世界的认识整理出来一个有线索有基础假设的结构。

在具体操作的层面，问“主要信息或者主要结论或者主要论点是什么(What)”、“如何论证或者操作来证明这个主要信息结论或者论点(How)”、“为什么这样论证，为什么论证这个(Why)”、“这个信息以及这个论证的过程对我有什么意义(Meaningful)”这四个问题——我称为WHWM问题——通常会有帮助。有的时候，你需要不断地追问为什么。例如为什么苹果落下来，不是飞上天去？因为有引力。为什么有引力就会落下来？其他东西也会落下来吗？引力具有什么特征？怎么测量？为什么有引力，引力来自于哪里？为什么有了物质就会有引力？物质是什么？怎么测量？为什么能够这样测量？

一个基于以上理念的教学设计需要包含：

1. 课程目标：课程所在学科的大图景，以及这个大图景对于课程目标的意义。
2. 课程概念体系：用概念地图的形式呈现的课程主要概念和主要概念之间的关系。这张图要在能够反映核心概念和核心理念的基础上，内容越少越好。
3. 目标和体系的分解和实现：按照课程目标把课程概念体系做拆分和展开，设计好模块。所谓模块就是反映某个或者某几个课程大图景的可以用于教学的一群课程概念以及它们之间的关系。
4. 模块的具体课程教学安排：课的内容安排、形式、参考资料、作业题、反馈交流形式等。这个可以在实施设计的阶段在细化。不过魔鬼在细节之中，上面所有的设计依赖于这个具体教学安排。

我会有时间的时候就整理整理。打算从中小学数学物理开始。希望能够引出来更多的玉，尤其是语文英语政治历史地理生物等学科。同时，这样的一个概念体系实际上除了供课程设计使用，还可以用于内容标记，例如对习题的标记，对课本章节的标记，等等。有了这个标记，可以继续做很多深入的研究和服务。例如，考虑学生个体的诊断性考试。

那高中物理力学阶段，大图景主要是哪一些呢？

1. 什么是科学，科学方法论
• 发现现象或者问题
• 提出具体的（可检验的）问题
• 做实验或者计算来解决问题。在这里一定要突出批判性思维、系联性思考对解决问题的意义，以及技术进步和思维对于能够通过做实验推理和计算来解决问题的重要基础性意义
• 回答问题、应用
• 系统化：类似的现象和问题是否能够用类似的解决方式？如果可以，边界在哪里？进而形成原理和假设更少的更加统一的理论
2. 物理学的统一理论的梦：追求用一个东西（理论、方程、分析方法？）解释一切现象是物理学家的梦想
3. 力学世界观：事物的状态如何描述、会发生变化吗、变化的原因是什么？
4. 力学典型研究对象和问题：物体的运动，如何描述运动，运动状态会变化吗，变化的原因是什么？
5. 力学典型思维方式和分析方法（除了已经在科学方法论里面提到的实验、批判性思维、系联性思考和数学计算推导）：受力分析（矢量、矢量分解、注意坐标系的方向和实际运动方向的关系）、图形分析（速度－时间曲线和位移－时间曲线之间的转化）、单位可计算
6. 典型应用和其他学科的关系所有自然科学的基础（例如讲化学、地理学的时候要联系好，也可以物理老师来举例），数学是物理的语言，生活中的物理（具体讲课过程中一定要体现好这一条，让学生明白物理就是生活，不是和生活分开的）

下面是课程概念体系。我先用最简单的上下级关系来表示这些概念和概念之间的关系，更加一般的关系见下面的概念地图。

1. 首先，数学基础：矢量，坐标系，矢量的大小和方向，矢量的加法，矢量的分解和合成；几何，几种简单图形，三角形梯形长方形的面积计算，直线斜率的计算；带单位的四则运算。
2. 其次，时间、空间、坐标系、参考系、质点，在某个参考系下的某个坐标系下的时间空间中的一个质点在坐标。
   • 其中要注意一个非常细节和关键的问题，为什么质点只要保留质量这一个属性然后考虑其坐标就可以，不要颜色大小材料等其他属性。这个问题需要和动力学结合才能回答和理解好。
   • 在这里还有一个细节可以联系到前面的大图景中批判性思维、系联性思考还有技术对科学的促进的讨论：Galileo（伽利略）对于重物落得快的思辨和实验，以及钟摆的进步。其中思辨部分还可以继续深入，见《找到某事物成为某事物的特征（数学结构)》这个帖子。其中技术进步的部分，需要把计时器讲好。
3. 接着，牛顿第二定律、加速度、力。
• 第一定律是第二定律的推论、具体运动形式上的表现也是第二定律的推论。当然在这个推论的展示上，要注意逻辑过程，例如从加速度－时间曲线到速度时间曲线到位移－时间曲线。需要联系数学基础里面的面积和斜率。
• 更重要的事情是，一定要把当年Newton（牛顿）联系地上和天上，追问为什么，用数学来解决问题，得到比较统一的理论，这个物理学的精神好好讲清楚，让学生有体会。
• 具体的几种典型力（弹力、摩擦力）的来源、方向、大小也需要介绍一下。主要讲清楚道理，其他的留给作业去巩固。摩擦力的方向的问题需要做几道例题，强调如果没有力的时候的运动方向。
• 具体通过实验总结出来牛顿第二定律，也可以从科学方法论——做实验的角度来阐述。
• 力的合成和分解需要联系数学的矢量概念，需要注意受力分析的技巧，分解合成坐标方向的选择需要考虑物体的运动。
4. 物理量的单位和数值是可以同时计算的，这个需要特别强调一下。测量的时候的有效数字也可以在这里提一下。

高中物理力学第一册（参考人教版教材）概念地图

如果你想访问cmap格式的概念地图文件，它在这里。

如果把概念之间的丰富的联系去掉，仅仅保留上下级关系，类似于包含关系，则得到
如果你想访问cmap格式的概念地图文件，它在这里。

这两个图的最大的不同在于后者是两棵树，前者是一张网。

分解的小图和实际课堂设计，就不在这里列出来了。

第二册力学部分把牛顿第二定律进一步用在了更多的运动形式上，并且推导出来加速度的表达式、能量守恒的条件、动量守恒的条件。其中动量守恒还会用到矢量性，也就是哪个方向上合外力为零或者外力远远小于内力，则那个方向上满足动量守恒。这个对于理解矢量性是很有意义的。当然，整体上，让学生经历一下建立从牛顿第二定律为基础的理论体系，也是体现物理学家的统一梦、系统化梦的重要例子。因此，这一部分在概念上，没有太多新的东西。我把概念地图和层次关系概念结构图分别放在这里。注意：有些问题可能推导计算比较复杂，可以不做考试要求，但是从逻辑上是要明白的，例如匀速率圆周运动的加速度的推导。其实这个例子很有趣，需要用到弦切角定理，很好玩，充分体现数学和物理的关系。当年Newton（牛顿）就面对过同样的问题。速度方向和轨迹的切线的关系，以及速度大小和x-t图里面的切线的关系，要注意，不要搞混。

如果你想访问cmap格式的概念地图文件，它在这里。

如果你想访问cmap格式的概念地图文件，它在这里。

剩下的人教版教材还有两册电磁学，一册热学，一册波动力学，一册原子物理加上量子简介加上动量守恒。就暂时不整理了。目前这套书里面量子那部分的概念不是十分准确，量子力学和经典力学的区别不在于一个是确定的一个几率的，或者说，书里面所用的概率波，真正的区别在于一个是确定的或者概率波（确定也是概率的特殊情况，因此，可以统称概率波），一个是概率幅的波。

看了张鹤老师的书《数学教学的逻辑——基于数学本质的分析》，总结整理在这里。

首先，这本书的理念是：数学教学需要解决“教什么”的问题，解决了之后才是“怎么教”的问题，最后才是细枝末节的课堂活动组织、用什么设备来上课之类的纯教学技术问题。

其次，在教什么这个问题上，这本书主要阐述了要找到和确立学科思想，整理好知识的内在逻辑，围绕这个思想和逻辑来解决教什么的问题。

接着，这本书还举例整理了初中高中阶段的具体数学知识的逻辑体系。在整理逻辑体系的时候，运用的基本上是思维导图（作者叫做结构图）的形式。不过，你如果自己细看，你会发现，这些思维导图里有专门表示关系的“概念”。因此，实际上，作者有一些自发的对概念地图的运用。

其中作者用了有几个作者觉得讲课讲得很好的老师的例子来说明，讲课主要是关于教什么，怎么教的问题可以很平淡，只要思想上境界够，启发学生投入思考，做到教得好完全没有问题。

这些，我都是非常赞同的，甚至都可以当做我的《教的更少，学得更多——概念地图教学和学习方法》的例子。教什么永远比怎么教重要，比怎么才能用技术形式抓住学生注意力之类的上课的技术重要。

不过，说完了好的，就轮到不足了。这样的不足当然有点吹毛求疵，不过为了更加促进作者和读者的思考，我觉得还是有必要把这个不足提炼出来。不得不说，非常遗憾，作者对于数学本身的视野和理解，尽管对于中学老师已经是很高的境界了，限制了对“教什么”更好的回答。这个牵涉到“数学是什么”的问题。建议作者去看看下面的两本书，还有其他Ted　Talk的视频。当然，我的书也值得看看，其中有专门关于数学教什么的讨论。

1. Bender 《An Introduction to Mathematical Modeling（数学模型引论）》
2. Gowers《Mathematics: A Very Short Introduction（牛津读本数学）》
3. Chris Anderson: Questions no one knows the answers to，好奇心、科学和教育
4. Marcus du Sautoy: Symmetry, reality’s riddle，世界中的数学，尤其是对称性
5. Roger Antonsen: Math is the hidden secret to understanding the world，关于“理解”和数学，以及数学作为现实的表示
6. Conrad Wolfram: Teaching kids real math with computers，数学的四个阶段（提出问题、抽象化、计算求解、验证和提高）和当前数学教育以及可能的解决方案
7. Dan Meyer: Math class needs a makeover，数学教育和粗糙问题的关系

数学是思维的语言，是用形式语言的方式把思维明确地表达出来。大多数时候思维的对象是现实的世界，或者人的心智对现实世界的抽象。因此，尽管没有必要真的有联系，数学所表达的内容本身，经常和现实是有关系的。按照这样的数学是什么理解，我们发现，对一个问题做数学的思考需要分成几个不同的阶段：从现实问题中受启发的阶段，也就是提出问题；把提出来的问题变成一个数学问题的阶段；通过逻辑推理和计算来求解数学问题的阶段；把答案用到原始的问题中来检验的阶段。当然，后者基本上是科学家在做。数学家也做一些。如果结果不相符，还要回去修改之前的提出问题、数学化问题、求解问题的阶段。

分成这样四个阶段之后，我们再来看，数学课堂现在大多数时候在做什么，应该做什么。我们发现，绝大多数时候，数学课堂在教你第三个阶段——通过逻辑推断和计算来解决已经数学化之后的问题。对于提出问题、数学化问题和答案的检验，基本上不涉及。甚至，绝大多数时候，本来有这个教学目的的应用题，也是已经数学化之后的问题。因此，数学首先要教数学化，抽象化的能力，也就是从现实中从粗糙的问题里面提炼数学问题的能力，做简化假设的能力。当然，在解决数学问题的阶段，也有一些数学思想，例如大到数学归纳法——看看逻辑起点怎样，再看看能不能建立一个链条；例如小到代数的思想——习惯用符号来表示关系，而不仅仅是具体数字之间的计算；再例如小到代数表达式和图形的结合；再例如大到用集合和群论来看整个数学。但是，这些数学解决问题的思想，都赶不上提出问题和数学化问题的地位。

有很可能，其实你的数学课连第三个阶段都没有好好教你，仅仅是在教你第三个阶段的形式：把别人已经提出来的如何计算如何求解的过程，练熟了。这就是更大的悲哀了。如果说，一个数学老师能够让你体会这个第三阶段的思考过程、数学思想，那么，他\她已经算不错的老师了。很有可能这些你都体会不到，只能够做到学会计算的过程，然后，从不断地重复这个过程之中，来学会解题，于是获得好成绩。

因此，顺便提一下，所有教孩子们“\(1+1=2\)”而不讲清楚加法的含义和前提的家长们，你们就是在毁灭孩子的数学思维。加法的含义就是把具有每种同样单位的东西合起来的数量，而不是真的把东西本身合起来。前提就是需要被加起来的东西具有每种同样的质，同样的单位。孩子一旦理解这个，算加法，还不是分分钟就能学会的事情（再加上明白\(1,2,3，\cdots\)的含义，而不是记住并且能够从\(1\)数到\(100\)）。

有了这样的数学是什么，教什么的理解之后，我们就可以来整理一下中小学的数学知识的内容，围绕着这些核心理念，重新来讨论怎么教，教材怎么写的问题。

前面的帖子我已经批驳过小学老师的长方形和正方形的概念上的严重的问题了。有的老师还辩解说，小学阶段搞清楚这个概念上的包含关系有难度，所以，两种理解——选择长方形的时候包括和不包括正方形的图——都算对。有的老师还更进一步说“正方形是特殊的长方形”，因此肯定就不是“一般的”长方形，所以，名正言顺地不能算进去。

这个让我非常气愤。这是什么逻辑？就这样还要教数学？数学是关于思考的科学，逻辑和计算是非常重要的思考的形式。今天的一个例子，更我对这句话更加生气，起决定写个帖子呼吁废掉这句话，至少在课堂上不推荐使用，或者说推荐避免使用。

今天我问心儿：长方形和正方形什么关系啊？什么样的长方形是正方形啊？心儿回答说“正方形是特殊的长方形”。很好，再稍微想一想就能理解正确了。我等待着后半个问题的答案。过了半天，心儿说，不知道。

于是，我发现，心儿是记住了这句话，但是却没有思考这个“特殊”指的是什么，特殊在哪里。这就是机械式学习的典范：记住了一句话，却没有思考和懂得这句话的意思。包括上面那个这样辩解的老师，也没有搞懂这句话的意思。A是B的特殊情况的意思是说，A肯定是B，但是需要加上额外的也就是“特殊”的条件才能成为A，于是B不一定是A。凡是遇到这样的情况，学习者一定要搞清楚这个加上去的特殊条件是什么。在这里，也就是，“四条边都相等”，而不仅仅是长方形的“对边相等”（同时角是直角）。

等心儿搞清楚这个问题，我提示，那么“长方形是不是平行四边形的特殊情况”？心儿说是，而且特殊在“角是直角”，而不仅仅需要平行四边形的“对边平行”。

于是，问题来了，如果我们需要强调和记住“正方形是特殊的长方形”的话，为什么我们不同时强调和记住“长方形是平行四边形的特殊情况”，“平行四边形是四边形的特殊情况”，“整数是小数的特殊情况”，“小数是数的特殊情况”等等等等啊！

根本上就是一个集合的包含关系而已！完全没有必要强调“特殊”情况。如果想强调，所有的集合包含关系都强调一下去。所以，我非常讨厌“正方形是特殊的长方形”这句话，本身不能一以贯之（也就是所有的集合包含关系都强调一下“特殊”情况），使得学习者没逻辑，不思考，尽管本身没错。

另外，我特意去看了一下教材的所有细节，完全没有具体的定义。没有定义从好的一面来理解，不对学生的精确理解作要求。从不要的一面来理解，就是，完全没有企图把学生教懂。学习就像拼图，不能缺关键的几块，缺关键的一环，缺了也就支离破碎了，学起来更难了。这种平庸化的教学和教材，完全是违背认知规律的。深入才能浅出，当然，可以允许一部分学生深入不进去。但是，一定要给一部分学生深入的机会，学的更简单更透彻，实现“教的更少，学得更多”的机会，实现“学习的更少，学到得更多”的机会。

这是心儿画的关于这个四边形问题的概念地图（经过我的修改）：

这是心儿画的关于三角形的概念地图（其中的长程连接是我添加的，中间那个奇怪的关系也是我添加的）：

顺便今天跟心儿一起画概念地图，我们总结说作图需要考虑以下几个问题：是什么，什么关系，什么结构。我下次上课讲如何画概念地图的时候跟学生们分享。