前面的帖子我已经批驳过小学老师的长方形和正方形的概念上的严重的问题了。有的老师还辩解说,小学阶段搞清楚这个概念上的包含关系有难度,所以,两种理解——选择长方形的时候包括和不包括正方形的图——都算对。有的老师还更进一步说“正方形是特殊的长方形”,因此肯定就不是“一般的”长方形,所以,名正言顺地不能算进去。
这个让我非常气愤。这是什么逻辑?就这样还要教数学?数学是关于思考的科学,逻辑和计算是非常重要的思考的形式。今天的一个例子,更我对这句话更加生气,起决定写个帖子呼吁废掉这句话,至少在课堂上不推荐使用,或者说推荐避免使用。
今天我问心儿:长方形和正方形什么关系啊?什么样的长方形是正方形啊?心儿回答说“正方形是特殊的长方形”。很好,再稍微想一想就能理解正确了。我等待着后半个问题的答案。过了半天,心儿说,不知道。
于是,我发现,心儿是记住了这句话,但是却没有思考这个“特殊”指的是什么,特殊在哪里。这就是机械式学习的典范:记住了一句话,却没有思考和懂得这句话的意思。包括上面那个这样辩解的老师,也没有搞懂这句话的意思。A是B的特殊情况的意思是说,A肯定是B,但是需要加上额外的也就是“特殊”的条件才能成为A,于是B不一定是A。凡是遇到这样的情况,学习者一定要搞清楚这个加上去的特殊条件是什么。在这里,也就是,“四条边都相等”,而不仅仅是长方形的“对边相等”(同时角是直角)。
等心儿搞清楚这个问题,我提示,那么“长方形是不是平行四边形的特殊情况”?心儿说是,而且特殊在“角是直角”,而不仅仅需要平行四边形的“对边平行”。
于是,问题来了,如果我们需要强调和记住“正方形是特殊的长方形”的话,为什么我们不同时强调和记住“长方形是平行四边形的特殊情况”,“平行四边形是四边形的特殊情况”,“整数是小数的特殊情况”,“小数是数的特殊情况”等等等等啊!
根本上就是一个集合的包含关系而已!完全没有必要强调“特殊”情况。如果想强调,所有的集合包含关系都强调一下去。所以,我非常讨厌“正方形是特殊的长方形”这句话,本身不能一以贯之(也就是所有的集合包含关系都强调一下“特殊”情况),使得学习者没逻辑,不思考,尽管本身没错。
另外,我特意去看了一下教材的所有细节,完全没有具体的定义。没有定义从好的一面来理解,不对学生的精确理解作要求。从不要的一面来理解,就是,完全没有企图把学生教懂。学习就像拼图,不能缺关键的几块,缺关键的一环,缺了也就支离破碎了,学起来更难了。这种平庸化的教学和教材,完全是违背认知规律的。深入才能浅出,当然,可以允许一部分学生深入不进去。但是,一定要给一部分学生深入的机会,学的更简单更透彻,实现“教的更少,学得更多”的机会,实现“学习的更少,学到得更多”的机会。
这是心儿画的关于这个四边形问题的概念地图(经过我的修改):
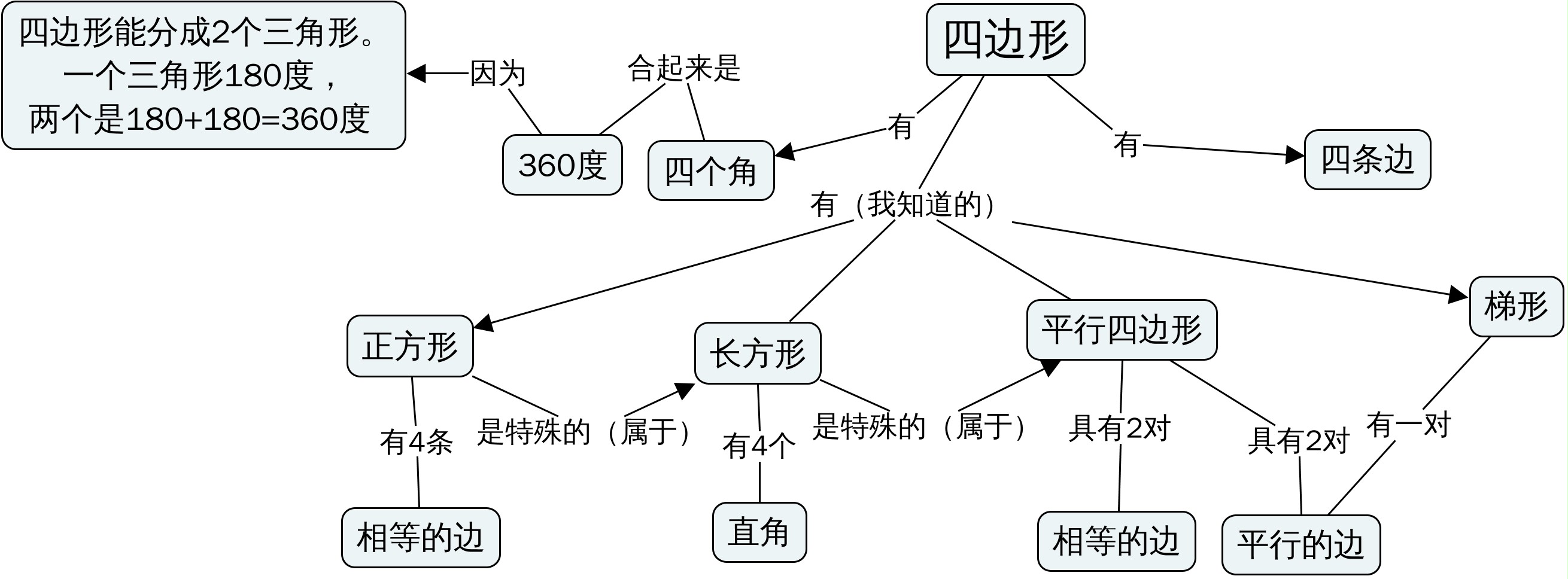
这是心儿画的关于三角形的概念地图(其中的长程连接是我添加的,中间那个奇怪的关系也是我添加的):
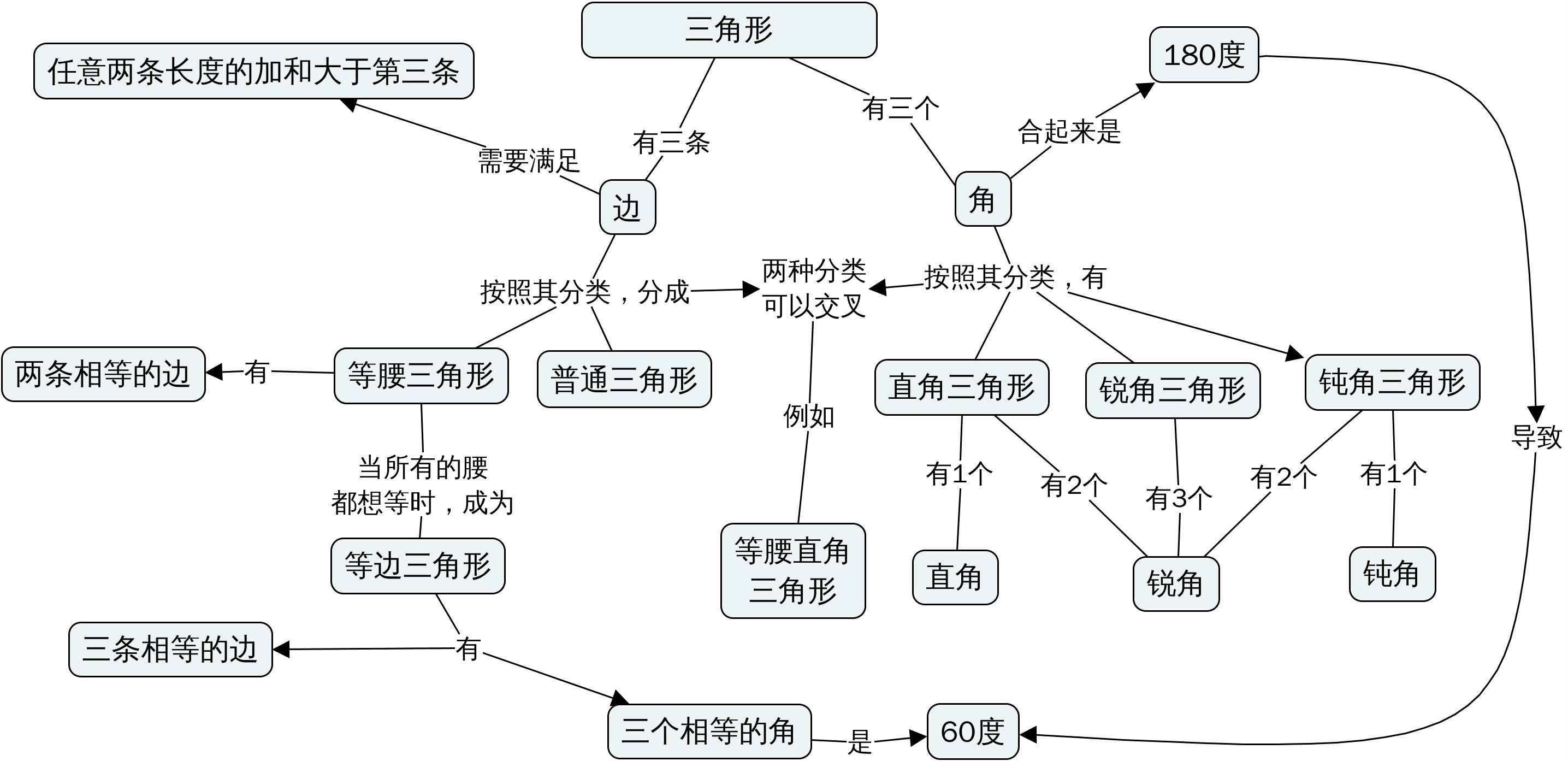
顺便今天跟心儿一起画概念地图,我们总结说作图需要考虑以下几个问题:是什么,什么关系,什么结构。我下次上课讲如何画概念地图的时候跟学生们分享。
反过来问一问更有意义,即增加什么条件就变成特殊形式,有利于真正理解。