月度归档： 2017年5月

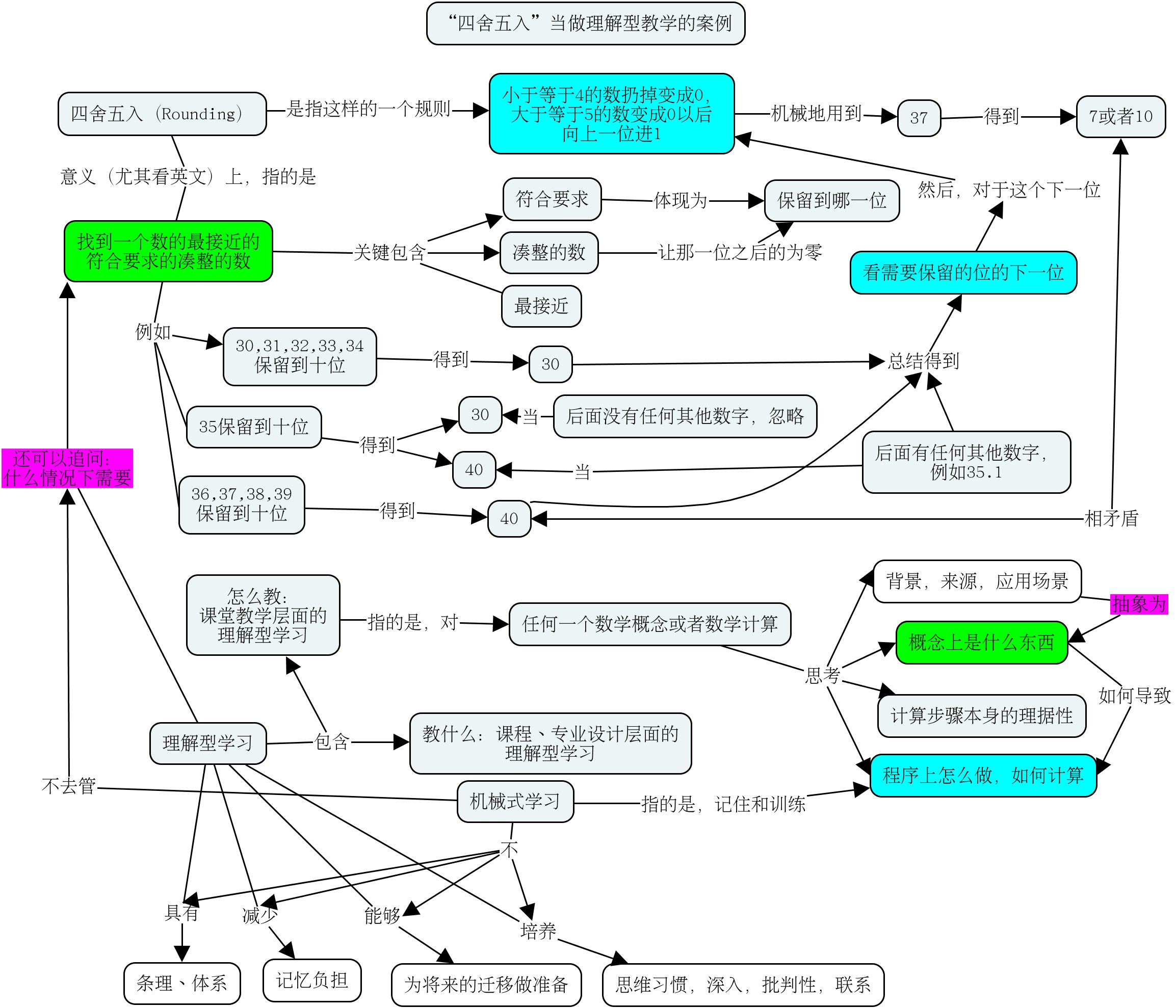
今天问起来心儿什么是“四舍五入”，回答说“凡是小于等于4的变成零，凡是大于等于五的自己变成零之后往前进一”。这个看起来似乎没错，可能书上都是这么说的。按照这个规则，我出了一个题：对\(37\)做四舍五入。在这里我特意避开了保留到哪一位的说法。

心儿回答\(40\)。我问，这个答案是否严格用了上面的四舍五入的规则。我演示，如果按照这个规则，我们来看这两个数，十位数是\(3\)，小于\(4\)，所以去掉变成零；个位数是\(7\)大于零，自己变成零之后往前进一，得到\(10\)或者保留\(7\)。因此，答案就是\(10\)或者\(7\)，而不是\(40\)。你看对不对？心儿说，肯定不对，但是不知道怎么回事。

这个事情的根源在于，“四舍五入”的规则在这里被强行记住了，但是没有明白这个规则怎么来的，是用来解决什么问题的。实际上，这个规则的目的是给一个数找到一个接近的凑整数。这个凑整数可以是保留到任何一位的。例如，保留到各位、十位、百位，甚至十分位等等。

理解了这个之后，“四舍五入”的具体规则可以自己构建出来，并且明白，对“\(5\)”的处理其实是有点问题的，尽管问题不大。\(30-34\)更接近\(30\)，\(36-39\)更接近\(40\)，\(35\)去哪边看起来都有道理。

到这里，可以总结：从概念上，“四舍五入”是为了寻找接近给定数的保留给定位的凑整数；从技术上，需要看保留位之后的一位的数值，如果这个数值小于\(5\)则变成零，如果这个数值大于等于5则变成零之后往需要保留的那一位上进\(1\)。

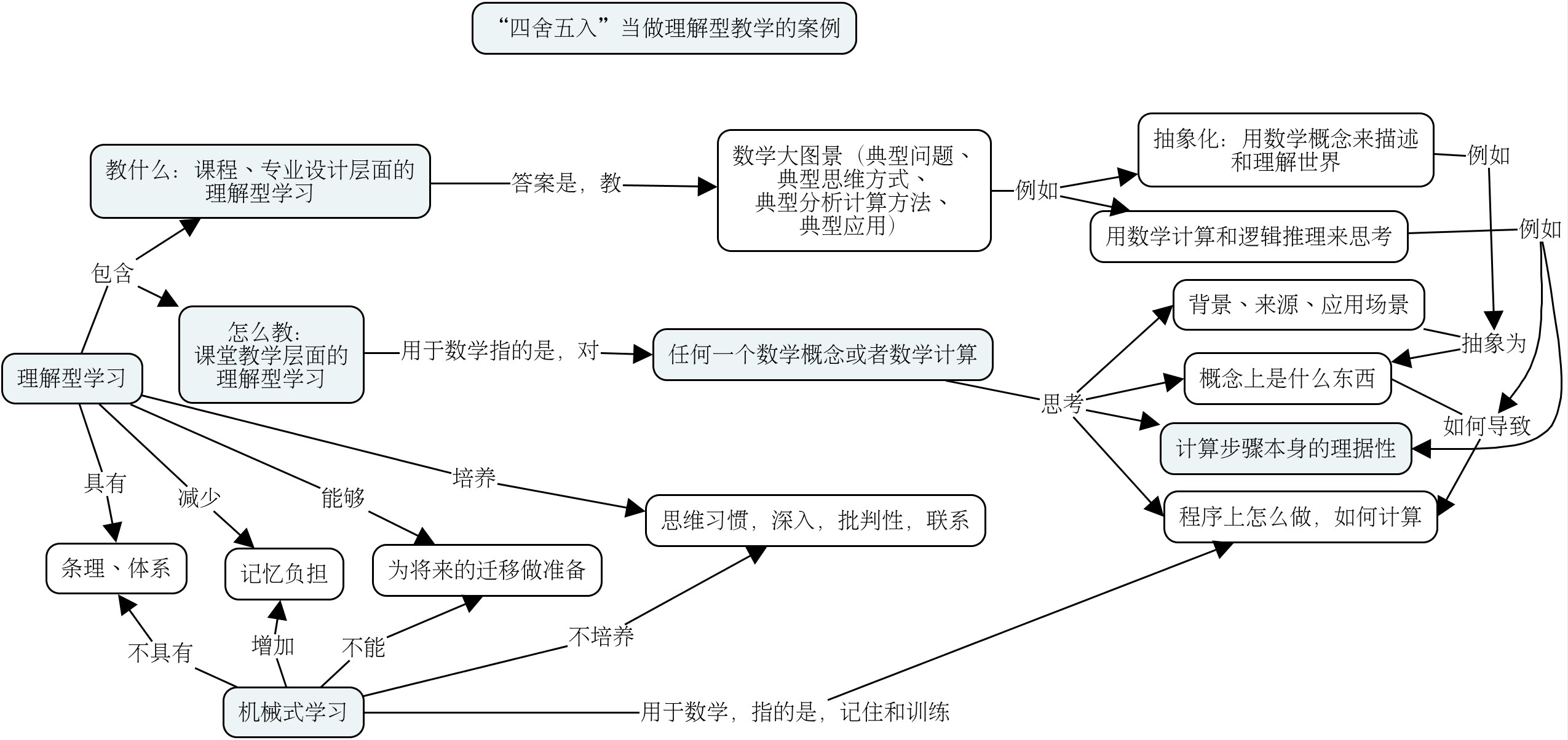
学数学和教数学，一定要把是什么和怎么做分开，并且主要关注是什么，最好还能够从是什么把怎么做想出来。

那么，这样学会的四舍五入有什么好处呢？第一，更加系统化。需要独立记忆的内容变少了，很多事情可以组织起来，联系起来了。第二，可以很好地迁移。例如，将来就会遇到保留到两位小数这样的问题，这个时候，就可以迁移过去了。第三，可能会用到更深刻的地方，例如，将来的测量读数的问题，而不是仅仅会做标明了四舍五入的题。而且一旦考虑测量和读数这个事情，就会发现，确实遇到\(5\)的时候进位更加合理：这个时候大多数时候后面还会有一点点其他的数，因此整体来说大于\(5\)后面直接是\(0\)的可能性居多，于是更加接近进位之后的那个数。第四，养成这样的通过思考和联系来学习的习惯，受益无穷。当然，也会有更多苦恼。

这也是一个具体课堂教学层次的“基于概念地图的理解型学习”的例子。其他的例子还有“分数除法”、”小数的加法“，“语言的魅力”、“从“欲速则不达”语文理解型学习的例子”

以下是这个帖子的概念地图型总结。其中，有一些连边，考虑到图的可读性，去掉了，换成了颜色对应关系。

更简化的图是这个样子的：

一直我都在培养心儿用自己的话来简单总结课文以及其他阅读材料，还有上课内容。这样的总结可以不用材料里面的任何原话，但是需要把主要意思保留下来。也就是概括主要信息是什么，这个意思是如何构建的。有的时候，我也会问：为什么表达这个意思，为什么这样来构建这个意思，以及最终的问题对读者的意义是什么。也就是我一直说的WHWM——What, How, Why, Meaningful。

今天遇到一个问题，需要搞清楚一句话里面的某一个词具体描述的对象是什么：“希望工程被公认为20世纪90年代中国人为改善教育落后面貌付出爱心的一块丰碑”，里面的丰碑是对什么东西的描述。由于这句话不是一般地长，而且主要意思有语法上不太正确的地方，因此就很难搞清楚丰碑是对谁的描述。

真的正确的话应该这么说：“希望工程被公认为是关于20世纪90年代中国人为改善教育落后面貌付出爱心的一块丰碑”。这样也就知道了中间的所有的从“关于”开始到最后的“的”都是为了更详细地说明“丰碑”，于是，这句话的缩写就成了“希望工程是丰碑”。于是，也就清楚了“丰碑”描述的对象是“希望工程”。

于是，我就希望教一教心儿学会结构形缩写。在不能介绍主语谓语宾语的条件下，说明白结构性缩写是有难度的。我尝试这么定义结构性缩写：采用原话的字词，只能去掉一部分字词，不允许调整顺序，不允许添加，尽可能短的，保留原话大概意思的缩写。例如，“肚子饿扁了的吴立心高高兴兴地吃了一顿非常非常非常非常好吃的吃了就能成仙能够上天入地的意大利面”，可以缩写成“吴立心吃了一顿意大利面”，进一步改写成“吴立心吃了面”。吴立心是主要人物得留着，吃是主要动作得留着，面是主要对象得留着。但是，心儿一直想不通，说应该缩写成“吴立心吃了一顿好吃的”。对于心儿来说，吃的什么是次要的，吃的东西好吃是最主要的信息。我花了很长时间没有想明白问题所在。

后来，终于明白，差别在我一直让她做的意义性缩写和这个结构性缩写。在意义性缩写里面，用什么话来说，是完全自由的，抓住自己认为的主要意思就可以。但是，在结构性缩写里面，需要保留原文的字词和字词的顺序，尽管也需要抓住主要意思。

了解这个差别之后，再尝试一个例子，“吴立心的优秀品质是坚持”，意义缩写就是“吴立心很坚持”，结构缩写就是“品质是坚持”。

刚才收到一位老师的“教小数加法”的一个好例子，说教材和老师都没有区分好“小数点对齐”（也就是位点对齐）和“末位数对齐”。在整数加减法竖式计算的时候，确实这两个对齐得到的结果一样，没必要区分。在整数乘法的时候，实际上不一样，但是被通常所教的计算过程——也就是拿出来十位数来相乘的时候，得到的结果的最后一位从十位数开始——掩盖了。到了小数加减法（其实乘除法一样的）的时候，就不得不做区分了，要不然会算错。因此，教材和老师用的例子应该体现出来这个差别，例如不应该用\(4.25+7.35\)而应该用（或者加上）\(4.25+7.3\)这样的例子。

这个老师注意到的事情是很有价值的。细节上，可以先让学生们犯个错，然后在老师的指导下跟学生一起来改进，并且讨论为什么要改成正确的那个计算过程。这个会很有意义。

这当然，已经是很好的课了。但是，按照我们理解型学习的要求，还有进一步改进的余地。第一，问为什么这样算，也就是计算过程的理据性。第二，问为什么对这个场景要用这个计算。

对于第一个问题，可以用乘法当例子：
\begin{align}
5\times 27 = 5 \times \left(20+7\right) \\ = 5 \times 20 + 5 \times 7 \\ = 5 \times 7+ 5 \times 2\times 10 \\ = 35 + 10\times 10
\end{align}
其中最后的那个\(10\)在竖式计算的时候被省略了，但是要求把这一个行的计算所得到所有的数往左边移一位（因为后面有乘以\(10\)）。同理可以得到百位数乘法的时候为什么所得到的末位数要和百位对齐：就是省略了那个额外的\(100\)。这样学生就能明白竖式计算为什么要采用这样的规则。

如果你关心更具体每一步的想法，它们是这样的：第一步，是为了把十位和百位拆开，将来好和竖式计算对应；第二部就是乘法对加法的分配律；第三步，按照竖式计算的顺序先计算个位的，然后计算十位的，其中十位的要当做个位来计算（将来要把算出来的结果左移一位）；第四步，为什么十位数上算出来的结果需要左移一步。

对于第一个问题，如果用小数加法当例子，则可以思考类似下面这样的问题：你的爸爸给了你\(1.5\)元，你妈妈给了你\(2.25\)，问你合起来拿到多少钱。启发孩子们用之前学过的圆角分做计算，可以知道：元需要和元的数目加起来，角需要和角的数目加起来，分需要和分的数目加起来。于是，分别得到3元，7角，5分。重新合起来，就是\(3.75\)元。这个时候，经过提醒，或者多做几道题，就可以帮学生总结，关键就是点位对齐，也就是小数点对齐，而不是末位对齐。

如果这个时候，老师再启发一下思考，为什么要把“元和元的数目相加，角和角的数目相加，分和分的数目相加”而不是混起来，就会从为什么能这么算，过渡到，为什么要这么算，每一步算出来是什么，这个第二个问题的层次。

对于，第二个问题，需要老师制造一个场景，来让学生自己想起来这里需要计算\(5 \times 27\)（运用乘法实际上就是加法的简便计算的理念），让学生们自己想起来为什么爸爸妈妈给的钱需要加起来。我们就不再设计这样的情景了。请读者结合昨天的帖子“分数除法的理解型学习和教学”来做自己的设计。注意，目的，是为了让学生一定程度上领会把问题数学化、抽象化的过程，从而思考为什么要这样算，而不仅仅是会计算。

理解了为什么用这个计算，为什么这个计算的过程是这样的，然后学会计算，才是理解型学习，才容易迁移，才能够学会用计算来表达自己的思想。

这个例子展示了，关于如何帮助学生思考计算背后的东西，也就是这样算的道理，以及为什么这个情境下用这个计算。也就是，在教学环节的细节的层次如何使用概念地图理解型学习，如何多问为什么，如何关注大图景（典型问题、典型思维方式、典型计算分析方法、典型应用的例子），如何运用WHWM（是什么、怎么构建、为什么这样构建、为什么说这个、对读者意味着什么）。其他的例子还有分数除法的帖子。