经典和量子系统的行为和理论有很大的区别。一般认为经典的数学模型(欧式空间矢量、概率分布)是不能描述量子系统的。见经典和量子的区别。
之前我提出来一个训练机器学习来求解Schrodinger方程的研究计划,看看是不是仅仅通过问题和已知的答案,能够得到一个Schrodinger方程求解器。见训练学习机用来求解Schrodinger方程
不过,由于写成Schrodinger方程之后,量子力学太像一个经典方程了,因此,就算能够学得出来这样的求解器,也不奇怪。如果得到波函数,然后加入测量,得到的实验结果,能够通过学习器给出来,就真的非常奇怪了。
于是,我提出来从光学实验的仪器组合出发,给定训练样本:仪器、组合、实验结果,然后看看是否能够在未训练的实验上也得到和量子理论一致的结果。
如果证明能够学到,也就是通过从一堆实验仪器和过程以及相应的测量结果里面学习到的模型能够用来给出正确的另一套同样的但是顺序方向等细节不一样的实验装置的测量结果的话,倒是比较简单,当然意义非凡——相当于找到了量子系统的经典理论,也就是实现了隐变量理论的目标,如果我们的学习机还是经典的话;如果数据结论是反面的,那逻辑结论比较难办——很有可能是没有解决好,而不是方法和思路有问题。因此,需要做好一个对比:类似的经典的情况,机器学习能够完全学到没有任何问题,然后同时,对比量子的情况,学不到。最好再增加一个量子学习机的学习结果对比,如果量子学习机能够学到,经典学习机学不到,而且经典学习机在类似的经典问题中能学到。这样就能够稍微更加有说服力一点,尽管还是有可能不是方法和思路的问题。
具体研究计划如下
- 理论上,量子力学提供了三样东西来描述量子系统:状态矢量或者说密度矩阵以及投影测量的计算(在此,我们仅关心投影测量)、叠加原理以及什么情况下叠加原理可用、演化方程。所谓学习到量子力学指的就是学到这三样东西,或者说学到和这三样东西给出来的结果一致的某个东西。演化方程为了简单计,另外也可以相信如果学会了密度矩阵和叠加原理演化方程的部分更加容易学会,就暂时不考虑。
- 状态描述和测量在量子力学的语言下是这样的:量子系统的状态是密度矩阵\(\rho\),测量一个物理量得到的状态\(O\)是这个物理量对应着的算符\(\hat{O}\)的本征态之一\(\left|o\right>\),其概率是\(\left<o\right|\rho \left|o\right>\),测量后状态是\(\left|o\right>\left<o\right|\)。
- 叠加原理在量子力学语言下是这样的:如果一个量子系统有多种可能的状态,例如经过不同的路径上的装置到达同一个地点的自旋或者光子,则整体状态是两个可能状态对应的矢量的叠加态,也就是,如果\(\rho_{a}=\left|\psi_{a}\right>\left<\psi_{a}\right|\),\(\rho_{b}=\left|\psi_{b}\right>\left<\psi_{b}\right|\),则合起来的状态是\(\rho=\left|\psi_{a}+\psi_{b}\rangle\langle \psi_{a}+\psi_{b} \right|\)。由于这个叠加性的适用条件牵涉到是否不可区分,而是否不可区分牵涉到纠缠态和部分迹,这一点,也可以暂时不考虑。当然,密度矩阵和矢量空间本身包含的叠加性已经体现在上面那一条里面了。
- 因此,整个所谓量子系统的行为能够不用量子力学而是用经典学习机来学到的问题,也就成了学习到能够用来给出正确的测量结果,并且这个测量结果不包含多条路径可区分的问题。于是,主要的实验结果就成了描述下面的量子系统的实验行为,当然其中这些磁场的方向可以随意更换。
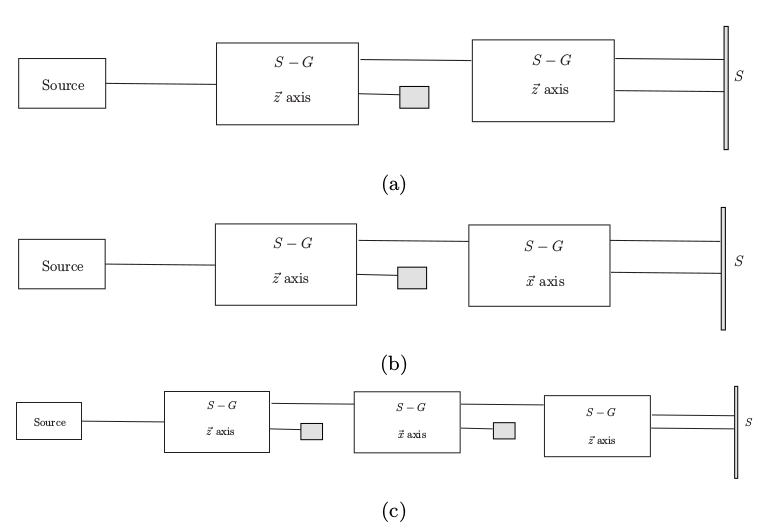
其中的实验(c)实际上是不能用任何经典理论来解释的:在制备阶段被消灭的状态后来在最后的测量中会再一次出现。
- 量子力学对这个问题的计算很简单:给定一个\(\left(\theta_{1}, \phi_{1}\right)\)方向的装置,挡住\(-\xi=\pm 1\)的一面让\(\xi\)的一面的光子进入下一步实验,则这个时候光子的状态是\(\left|\xi \hat{r}\left(\theta_{1}, \phi_{1}\right)\right\rangle\left\langle \xi \hat{r}\left(\theta_{1}, \phi_{1}\right) \right|\),它是算符\(\hat{r}\left(\theta_{1}, \phi_{1}\right) \cdot \vec{\hat{\sigma}}\)的本征值为\(\xi\)的本征向量,其中\(\vec{\hat{\sigma}}\)是三个Pauli矩阵。于是,如果这个状态,如果遇到一个\(\left(\theta_{2}, \phi_{2}\right)\)方向的测量,则测量结果可能是\(\eta = \pm 1\),其相应的概率为\(\left\langle \eta \hat{r}\left(\theta_{2}, \phi_{2}\right) \right|\left. \xi \hat{r}\left(\theta_{1}, \phi_{1}\right)\right\rangle\left\langle \xi \hat{r}\left(\theta_{1}, \phi_{1}\right) \right.\left|\eta \hat{r}\left(\theta_{2}, \phi_{2}\right)\right\rangle\),测量后的状态是\(\left|\eta \hat{r}\left(\theta_{2}, \phi_{2}\right)\right\rangle\left\langle \eta \hat{r}\left(\theta_{2}, \phi_{2}\right) \right|\)。
-
给定量子问题训练集:也就是上面的图(a,b,c),其中磁场方向可以任意,对结果做量子力学计算来得到结果并用结果来标注。进行训练。训练得到的学习机用来预测测试集的实验结果。也就是说,我们运用这几样东西——若干个某个方向的磁场,挡住某个方向的输出的物块——来组成任意的实验过程,机器学习的目的是给我们这样的实验过程的正确的结果——表现为最终向上和向下输出的概率。
-
作为对比,我们提供量子力学的计算框架,在已知这个计算框架的条件下来学习,看看经典学习机是否能够学到。也就是给定
\begin{equation}
\left|\xi \hat{r}\left(\theta, \phi\right)\right\rangle = \left[\begin{array}{c}\alpha \left(\theta, \phi\right), \beta\left(\theta, \phi\right) \end{array}\right]^{T},
\end{equation}
看看能否学习到这些函数\(\alpha, \beta\)。 -
给定经典问题和训练集:考虑一个经典多面体,其状态是多面体\(S\)中的一面\(s\)以及这些面的概率分布\(\rho\left(s\right)\)。有了这个多面体也就有了改变这个系统的状态的方式,也就是算符\(\Lambda\)——其每一个元素是\(s\)个状态的置换矩阵——和所对应的物理操作。然后,通过在给出来这些作用算符和测量算符的顺序并且做好结果标记的训练集上做训练,跟量子系统的学习一样,能够对新的算符的组合给出来正确的测量结果。
我们想看一看,是否经典系统的学习可以成功,量子系统给出来数学描述的需要学到函数的学习也可以成功,但是,量子系统的学习不会成功。如果真的是这样,那么,就表示,基于经典模型的学习机不能学到量子力学。
如果还能够给出来一个量子学习机的框架,并且学习成功,那么,就从一个全新的角度——让全能的经典学习机去试试——基本回答了量子隐变量理论的问题。