分类： 教学思想和技术

吴金闪对教育学科的认识和相应的课程设计

教育本身的目的就是发掘发现和培养学习者的能力，提升学习者思考和进一步学习研究的愿望。适当的时候，在帮助学生找到自己和认知世界的基础上，也鼓励一下贡献社会。科学中的反思怀疑是一切的基础，没有它就什么都没有。要通过教授科学来培养独立思考。创造是教育的功利性目的。为了保护培育创造性，除了批判性思维，还要有系联性思考，有的时候也要做点探索性学习。时间是稀缺资源，每一个学科都应该把学会大图景(基本问题，典型思考方式，典型分析方法，对知识结构的理解)放在前面，而不是细枝末节。考试要为了促进对大图景的学习，做好诊断的功能。必要的时候，除了探究性学习，也可以做中学。

其他的一些技术，例如同伴教学、讨论式教学、翻转课堂、在线课程等等也可以促进学习，但是，不解决教什么和内容上怎么教的问题，仅仅是关注形式上怎么教以及课程载体的问题。当然，在线课堂使得学生们获得好教师的可能性大大提高了，这个技术还是有很大的贡献的。

当然，这其中，没有一个是我自己的。从教育思想上说，以上的认识来自于Ausubel（奥苏贝尔）、Bruner（布鲁纳）、 Dewey（杜威）、Whitehead（怀特海），Novak（诺瓦克），也可以算上Piaget（皮亚杰），还有国内的陶行知，丰子恺等。如果说有我自己的地方，就在于，我提出来，可以在整体课程设计个别课程设计甚至个别课的设计等层面，运用概念地图，来做好以系联性思考、批判性思维为基础的以学科大图景为目标的理解型学习。

为了达到这个目的，必须对学习行为有好的研究，必须对具体学科有好的认识，还必须找到一定的从具体学科到具有一定普适性的教学和学习的路径或者说桥梁。因此，教育这个学科，如果还算得上是一个学科（一个学科通常需要核心的理论，基础的概念，基本研究问题，典型思维方式、典型分析计算方法，典型应用）的话，这个学科的核心理论也不在教育学，而在于对学习行为也就是脑科学的研究、对具体学科的研究以及从具体学科的研究理解到到这个学科的教学这个桥梁。当然，这三个方面都需要研究者。因此，勉强把这个群体算作教育学的研究者也是可以的。但是，要注意，原则上，第一第二两类都是自己学科的研究者，只不过是关心教学问题的脑科学和具体学科研究者。第三类，可能更像一个教育学或者应该叫做教学学研究者。不过，这个时候，研究的层次可能不是针对核心理论问题的，而更多地是工程层次的。也就是说，前两者相当于理论和实验物理学，第三个相当于电子工程师。也就是说根本就没有所谓的教育本体的问题，教育的本职任务是为学生和老师的学习和教学，为具体学科的传播服务。如果一个宣称自己是搞教育的研究者，自己课讲不好，不能帮助老师讲好，不能帮助学生学好，不能帮助学科传播好，算什么搞教育的。从学科上来讲，教育学科的基础也在脑科学（行为、心理、大脑）和具体学科，而没有自己的根本学科。

基于对教育和教学的以上的认识，我们（吴金闪、Novak、Canas等）设计了《学会学习和思考》教育学模块课程设计。稍后我也会把科学和科学教育模块的课程设计发在这里。

课程目标：
1. 刺激和引导学生思考什么是教育学，如何做更好的教育
2. 学生可以有自己的思考和理解，但是大概来说：教育学这个学科的根本任务是促进学习和教学，其学科基础是具体领域的知识以及人类学习、教学和思考的科学。
3. 了解和实践教育中一些好的理念：系联性思考、批判性思维、做中学、从教（同伴）中学习、项目和问题为基础的教学、粗糙问题的价值、教的更少学得更多。关注大图景——学科基本问题以及和现实的联系、典型研究思想和分析方法、核心概念以及它们之间的联系，问理据性等WHWM问题（W：什么是主要信息，H：这个信息如何通过概念例子以及它们之间的联系来表达，W：为什么你想表达这个信息，这个信息对于我还有这个世界意味着什么？），刺激挑战引导学生和学生平等讨论（让学生问他所想问，说他所想说）
4. 了解和避免一些教育中的一些不好的理念：用重复练习来代替对概念理解的深化、用忽略学生多样性的固定套路来禁锢学生的思考和创造性、仅仅关注抽象成模型或者数学问题以后的世界而忽略抽象化的重要性、按照习惯的教材或者教法来教学而不反思其理据性。
5. 对构建真的能够解决主要任务的教育学的兴趣
6. 学习和教学能力的提高
7. 在学习和思考“教育学”的过程中实践系联性思考、批判性思维，学会学习和思考

学习材料：
1. Ted Talks视频：
* Roger Antonsen: Math is the hidden secret to understanding the world，关于“理解”和数学，以及数学作为现实的表示
* Victor Rios: Help for kids the education system ignores，教学和教育中的心理建设，信任的力量，帮助的力量
* Tim Brown: Tales of creativity and play，创造力和玩
* Cameron Herold: Let’s raise kids to be entrepreneurs，创业者的特质和培养
* John Wooden: The difference between winning and succeeding，赢和成功和教育的关系
* Chris Anderson: Questions no one knows the answers to，好奇心、科学和教育
* Sal Khan: Let’s teach for mastery — not test scores，网络课程Khan学院的学习模式
* Carol Dweck: The power of believing that you can improve，教学和教育中的心理建设，鼓励的力量
* Christopher Emdin: Teach teachers how to create magic，教学本身需要创造性
* Peter Doolittle: How your “working memory” makes sense of the world，脑科学如何帮助学习和教学
* James Flynn: Why our IQ levels are higher than our grandparents’，IQ在检测什么这个什么和科学的关系
* Clint Smith: The danger of silence，让每个人都问你所想问，说你所想说
* John Green: The nerd’s guide to learning everything online，思考改变世界，人生就是探索未知世界
* Takaharu Tezuka: The best kindergarten you’ve ever seen，建筑改变行为和思维并促进学习和成长
* Anant Agarwal: Why massive open online courses (still) matter，网络公开课和现代教育
* Andreas Schleicher: Use data to build better schools，能力和潜力能够检测吗，检测结果能够用来促进教学吗？
* Daphne Koller: What we’re learning from online education，网络公开课和现代教育
* Peter Norvig: The 100,000-student classroom，网络公开课和现代教育
* Sal Khan: Let’s use video to reinvent education，网络课程Khan学院和现代教育
* Conrad Wolfram: Teaching kids real math with computers，数学的四个阶段（提出问题、抽象化、计算求解、验证和提高）和当前数学教育以及可能的解决方案
* Dan Meyer: Math class needs a makeover，数学教育和粗糙问题的关系
* Kiran Sethi: Kids, take charge，让孩子来当家做主改变世界
* Hans Rosling: Let my dataset change your mindset，数学可以很有趣并且改变你的思想
* Liz Coleman: A call to reinvent liberal arts education，什么是真正的通识教育
* Alan Kay: A powerful idea about ideas，精心设计的神奇的任务和计算模块帮助学习数学和科学
* Arthur Benjamin: Teach statistics before calculus!，按照其他人或者教科书来教学吗？
* Patrick Awuah: How to educate leaders? Liberal arts，通识教育和社会
* Richard Baraniuk: The birth of the open-source learning revolution，网络公开课和现代教育
* Ken Robinson: Changing education paradigms，Ken Robinson教育的问题和出路四重奏，创造性和现代教育的目的
* Ken Robinson: How to escape education’s death valley
* Ken Robinson: Bring on the learning revolution!
* Ken Robinson: Do schools kill creativity?
* Marcus du Sautoy: Symmetry, reality’s riddle，世界中的数学，尤其是对称性
* Cédric Villani: What’s so sexy about math? ，数学描述世界超越简单经验
2. Joseph Novak: Life experience and meaningful learning，通过Novak自己的生活经验来更好地理解概念地图、理解型学习
3. 供参考的公开课：
* 《Justice》by Michael Sandel
* 《Game Theory》by Ben Polak
* 《Quantum Mechanics》by Leonard Susskind
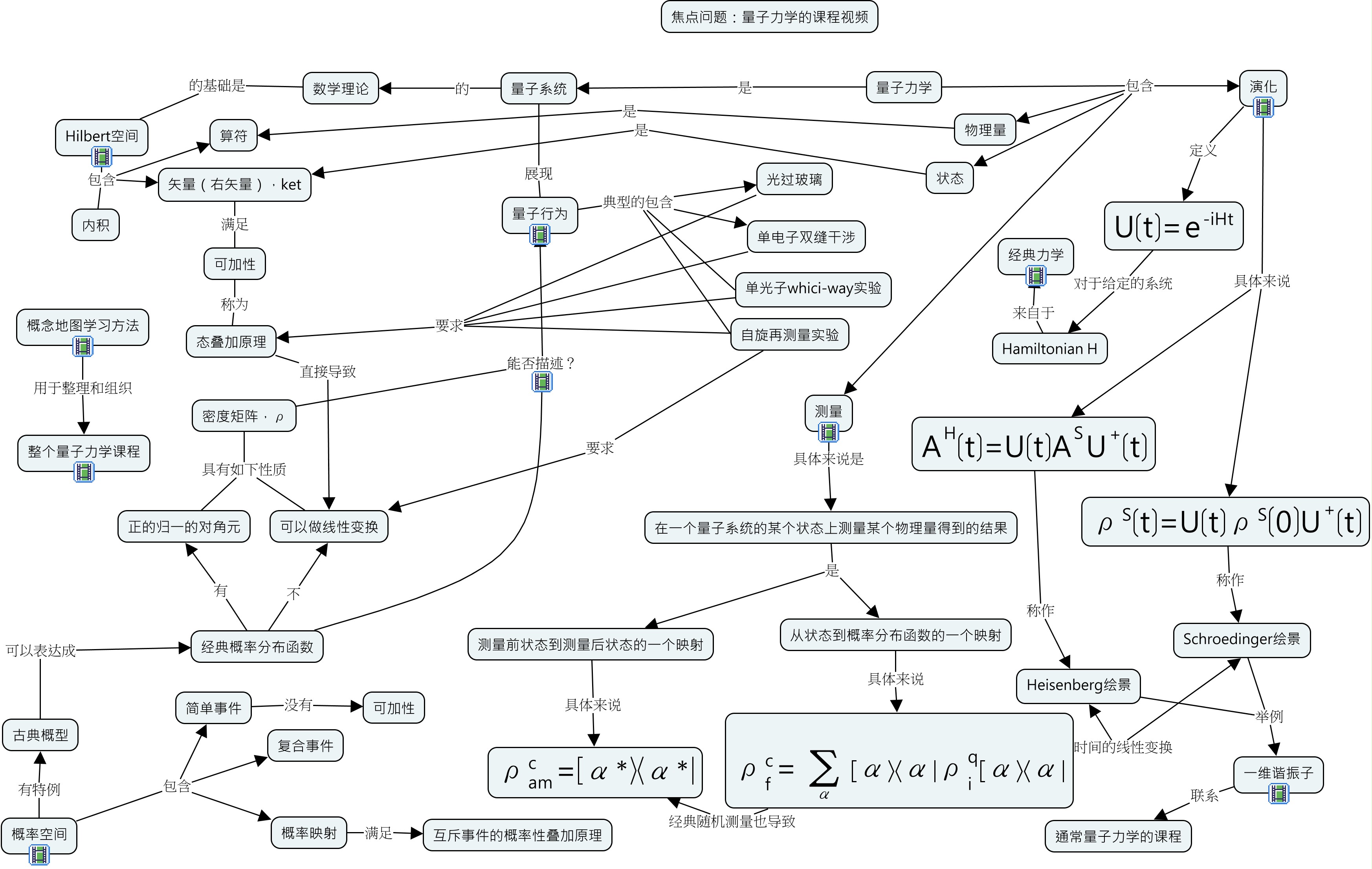
* 《量子力学》吴金闪
* 《系统科学导引》吴金闪
4. 书
* 吴金闪《概念地图教学和学习方法》
* Whitehead《教育的目的》
* Novak《学习、创造与使用知识——概念图促进企业和学校的学习变革》
* Bruner《教育过程》
5. 先修课：《学会学习和思考》技能训练模块，或者其他经过我们认可的概念地图和系联性思考培训班
6. 课程形式：在两周的时间内每周三次每次三小时集中上课，三小时老师授课（分享理念、举例子、讨论），学生看视频做口头报告和讨论
7. 对学生的要求：熟练的英语听说（课程为全英文授课）、对教育感兴趣并且有一个开放的头脑还要愿意接受理念和学习难度学习方式上的挑战
8. 课程主要作业：看所有的视频，选择其中的一个按照WHWM来做基于视频的“关于什么是教育学如何提高”的报告，按照“Teach Less, Learn More”的原则完成一门课的课程设计，完成课程报告——总结课程学到的内容并反思

反映内容逻辑的mooc平台系统

目前的mooc课程起到了给大量的学习者提供好老师好课程的作用，但是课程本身还是传统的授课方式。当然，技术上不乏使用讨论式教学等比较新的好的教学方式的课程。总的来说，没有根本上改变学习，改变教学。当然，这些好老师们一般在个体的层次都能够回答得比较好“教什么”、“怎么教”的问题，还能够体现其对整个学科的整体认识，整体面貌。整体面貌也就是通常说的结构，或者我说的学科大图景，包含基本问题、典型思维方式、典型分析方法，以及一些体现这个大图景的典型例子和为了给学生进一步学习准备的基本概念。因此，简单来说，就是有结构的学习和教学，学会对知识的整理、知识结构的理解，甚至这种通过结构来学习大图景的学习方法。当前的mooc平台并没有在系统平台的层面或者思想的层面，技术的层面，促进这个基于整体结构和大图景的理解型学习和教学。

在这一点上，我一直在推动和构建的“基于概念地图的理解型学习”具有非常大的促进意义。学生需要思考每一个概念之间的明确的联系，需要建立起来一个学科大图景。更重要的事情是，通过这个概念地图，老师可以更好地从概念之间相互联系的角度来决定教什么，按照什么顺序教，怎么教，学生可以摸索自己的学习顺序，决定学什么。

因此，我提出来，要建立一个以学科概念地图为基础的资源组织体系来构建和呈现课程：先把一个学科或者一门课程的主要概念拿出来，搞清楚概念之间的联系，制作出来学科或者课程的大概念地图，体现学科的大图景（基本问题、典型思维方式、典型分析方法），然后把教材的相应的章节、视频课程的每一个相应的概念、文献和其他资源整合到这个概念地图上去。当然，可以有不同详细程度的概念地图，也就是有嵌套。

这样，学生就可以自己来选择学习内容和顺序，并且在这个选择的过程中对于概念之间的相互联系有非常清楚的把握。

按照这样一个设计，做出来的产品大概是这个样子的：

QMwithVideo

或者，我也可以通过iframe直接把概念地图放到网页上。

但是，如果真的开发一个这样的mooc平台，则需要做一个网页呈现形式的平台，直接把这个概念地图和相应的概念和关系上的资源直接现实在浏览器之中。当然，为了开发方便，还需要一个能够把概念地图文件（可以输出成xml格式）直接转化成这个网页呈现形式的软件。

额外的功能还应该包含：直接在这个网页形式的概念地图上点击视频资源以后可以播放，可以就某一个概念或者联系来展开讨论。

这是根本性的学习的革命，从关注具体的一条条的知识，到关注对知识结构的理解，到用这种系联性思考来学习和思考。这是真的授人以渔的教学的革命。我希望找到合适的开发者，来建设这样一个系统。

目前，我们自己正在基于这个理念建设《系统科学导引》、《量子力学》等课程。《汉字学习》也在计划中。内容我们可以先做起来。平台系统的思想也已经在这里提出来。现在就缺乏开发这个系统的人和运营这个系统的人了。

做几门课，做一个平台的基本功能，用起来，然后，看看有没有可能拿到推广需要的资源，不管是来自于市场还是基金。

读《谈谈方法》和《社会契约论》有感

科学知识和科学精神不是一回事。科学精神需要通过学习科学知识来体现和体会。学习科学的主要目标却不是科学知识而是对科学知识的内涵、来源以及背后的原则的理解。这也是为什么我开设《学会学习和思考》：学会科学地思考问题，看待世界，远远比学会具体科学知识重要。当然，不经过具体知识尤其是对具体知识的体系化的整理和理解，根本就谈不上领会科学精神。具体学科的知识和具体学科的思考方法，每一个学科，都不一样。但是，很少的几样有共性的科学精神还是有的。那就是：怀疑和反思、构建一个（相容的尽量统一的假设尽量少的可计算的）心智模型来理解世界的企图、做实验和尊重事实、做计算（依靠数学来做逻辑推理）。

在物理学的发展而言，Plato的精神世界对应着现实世界（或者应该反过来说，甚至认为只有精神世界才是真实，现实世界仅仅是虚像）、 Socrates的思考和反思、 Aristotle企图建立物理学是什么（关于运动和世界怎么样，为什么的理论和思考）的体系、Descartes的怀疑是一切科学的基础（“我对我自己是否存在的反思证明我存在”、“我从来不把没有经过反复思考的东西当做真理”）、Bacon的经验主义和归纳，这些应该算作物理学建立的思想上的基础，也就是“怀疑和反思、构建一个心智模型来理解世界的企图”这一部分。而Galileo的实验和理想实验（确实对物理学具体知识的贡献已近非凡）真正使得物理学依靠做实验的方式从哲学中独立出来应该算是做实验和尊重事实这一部分。接着Newton对天体运动记录的深入思考以及把天体运动和Galileo的地上运动统一起来的万有引力模型和动力学方程以及表达动力学方程的微积分的提出，应该算可计算这一部分。所有的这些——怀疑反思心智模型做实验做计算——合起来是物理学也是现代物理学的基础，尤其是相对论和量子力学。物理知识进步了发展了变化了，科学思想仍然是一样的。这些有的时候也被称为科学方法论。

一直学物理，更加关注具体知识，直到有一天开始上课，才渐渐开始关心如何把自己对科学的背后的理解，对科学知识的来源和体系结构的理解，对概念之间的联系的理解，传授给学生，促进学生理解科学，理解科学的发展，甚至促进社会的进步。于是，开始看起来Whitehead和Descartes。强烈推荐每一个做科学的对科学感兴趣的教科学的都看看Descartes的《谈谈方法》和Whitehead《教育的目的》。其中，Descartes在《谈谈方法》以自身的理性思考的经验为基础提出来：
1. 从来不把没有经过反复思考和反思的东西当做思考的基础（怀疑反思）；
2. 把问题分解成更简单的小问题来处理（分析）；
3. 认识问题要有一个从简单到复杂的顺序，或者对于还没有这样的体系的东西也要建立起来这样一个顺序体系（联系、体系）；
4. 尽量反复全面地考察问题（一致性最少假设）。
科学不就是用这样的一个方式来考察世界得到的结果吗。Descartes不仅是一个思考者，他还把这样的思考真的用来发展具体的数学知识（解析几何）和物理学知识（光学）。除了批判性思维，Descartes在这里还提到了系联性思考。

一个学会了用这样的方式——批判性思维、系联性思考、心智模型、做实验、做计算——来认识世界思考问题的人，不仅仅能够更好地理解自然的世界，可能还可以促进社会的世界的进步。不过，这个时候，我开始想，学会了思考和学习，还差什么才能真的促进社会的进步呢？所为促进社会的进步，不是指你在这个社会里面混得如鱼得水，很自如，而是你思考问题所在你思考出路在哪里。这个时候，Rousseau的《社会契约论》就突然出现在我的脑子里：一个稳定的社会成为社会的基础是什么？一些个体为什么要一定程度上服从另外一些个体，或者服从另外一些个体所代表的集体？要知道，Rousseau他自己可不是一个统治者，也不算贵族，甚至不算大富，在当时以血统和权威作为基础的社会里面，怎么会开始一个关于统治权问题的如此跳脱的思考呢？例如，他论述强权不是社会的基础的时候，是这样说的：如果强权是基础，那么，当有人开始不服从并且获得了更加强权的地位的时候，是不是就反过来大家——包含之前的处于强权地位的个体，就要服从这个新的强权呢？于是，你看强权不鼓励服从啊。接着，他开始问既然强权不是基础，那么是不是有一部分人真的可以放弃一切呢，例如奴隶制社会的奴隶。这个时候，也许你可以认为已经有能力做出放弃的选择的成人可以放弃，但是就算如此，他们也没有权利代替他们的子女来放弃啊。于是，一部分人主动放弃一切权利主张也不是社会的基础。那么，到底什么是社会的基础？

你可以看到，在这个问题完全没有答案的时代，在这个问题甚至否没有提出的必要性的时代，Rousseau开始探讨这个问题，并且提供了一个可能的答案：契约。为什么他能够做到这样，怎么做到的，不过就是反思，不断地深入地反思。

一部分人已经能够吃饱饭了。让吃饱饭的人中的一部分思考起来，是我们教育者的责任。启发他们思考什么（看什么书），帮助他们做如何思考，是我们思考者的责任。

对了，说起来看什么书，思考什么问题，推荐大家，尤其是教育者，看看我的这本书《概念地图教学和学习方法——教的更少学得更多》。

刺客信条的信条：Nothing is true，Everything is permitted

电影《刺客信条》里面讲了刺客组织和圣殿骑士之间围绕着伊甸苹果的斗争。据说这个苹果里面包含了人类反叛的种子，只要研究清楚这个种子，就可以让人类顺服。圣殿骑士期望得到这个苹果并破解它。刺客，那帮信奉自由意志的人，希望保护和隐藏这个苹果。故事就是这么简单：看着刺客们为了保护和隐藏这个苹果一次一次地自不量力地冲上去，然后基本被消灭。

那，到底是什么信仰使得刺客们愿意牺牲一切呢？那是因为他们认为这是之所以成为人的基础。下文的资料来自于电影和这个有关刺客信条的网站。

When other men blindly follow the truth, remember…Nothing is true.
When other men are limited by morality or law, remember…Everything is permitted.

当其他人盲从所谓的真理，记住……没什么东西是不变的真理。
当其他人都被道德或者法律束缚，记住……任何事情都是允许的。

They never preached answers, but guided me to learn from my self. We don’t need anyone to tell us what to do. We are free to follow our own path. There are those who will take that freedom from us, and too many of you gladly give it, but it is our ablity to choose – whatever you think is true – that makes us human. There is no book or teacher to give you the answers, to show you the path. Choose your own way.

他们从不会直接提供答案，只是引导我去思考。我们用不着任何人来告诉我们做什么。我们有自由去寻找我们自己的道路。 总是有些人想要拿走我们的这种自由，并且，你们之中太多的人都很乐意把它给他们。但是，我们之所以成为人，就是因为我们选择的能力——我们选择那些我们认为是对的的东西的权利。没有哪本书或者老师会给你答案，或者给你指出一条路。选择一条你自己的路。

看完这个电影，当然，有其他的更深刻的思考，忽然之间，我想到当老师，想到教什么的问题，想到学什么怎么学的问题，想到怎么做研究的问题。

去思考，去选择，去反思，来反问，这就是学习。鼓励你去思考，接受你的选择，高兴看到你的反思，乐意被你反问，这就是教学和教育。一个连电影都懂的道理，教育界怎么会不懂。做研究工作更是这样，没什么是不可能的：大胆假设，仔细思考，谨慎推理，周密验证。去思考，去反思。

数学教什么，怎么教

刚才看到了一个讨论美国数学教育的“问题”和历史的帖子，想起来确实美国也搞教学改革运动，尤其是数学。

一开始可能大家都是关注basic，也就是学会计算就可以。这个是工业时代的教育观下的产物。工业时代我们主要需要能够执行管理者制定好的方案的工人，而管理者很有可能也是在执行更高层次的设计管理者制定好的方案等等等等。当然，方案和规则制定的时候可能有过科学研究实证研究。因此，这个体系也不是太差。基本上就是螺丝钉的思路，稍微好一点的可以给不同的螺丝钉一些选择的机会。但是，总而言之，社会就需要一系列不同的螺丝钉而已。这个思想下，语文主要是为了学会看懂说明看懂指导语，数学主要是为了数数做计算做测量等等。

后来，美国搞起来了新数学（New-Math）运动，把大量的现代数学加到中小学阶段的课程里面，而且，提出来，计算这样的基本的东西（basic）可以用计算器计算机来代替，不值得当做数学学习的中心。这个思想是很好的，绝对意味着进步。但是，实际操作很难，而且走偏了。在否定掉basic的同时，尽管提出来了一些需要树立的东西，但是不够明确，更加没有给出来如何树立这些东西。于是，新数学运动给中小学老师的指导语就是：计算不再是重要的了。那什么东西重要呢？没有提供，至少没有明确提供。那你可也想见这个有多么的糟糕。大量的老师和教学参考书把更高级的数学概念和数学计算搬到中小学。概念和计算高级了，就能够学到什么是数学了吗？根本不能。于是，新数学运动就被废了。

接下来，就遇到了非常困难的时期了，基本的不应该是主要教学目标，更好的更体现数学是什么的又没有，怎么办？于是一帮人提出来要back-to-basic，回去教计算得了。这帮人还挺得势，至少这样教出来的孩子会算题，考试成绩要高一点啊。要不然，你说怎么办？

这个“要不然，你说怎么办”的问题是一个大问题。其实，这是没有想象力，没有创造力，不懂得什么是数学的人，才会问的问题，也是那些懂得数学是什么有创造力和想象力的人没有尽责任影响数学教育界的问题。Whitehead在《教育的目的》，Timthy Gower在《数学是什么》里面都提供了对这个问题的思考和思考的答案。数学是思考的语言，数学为对现实的描述提供了结构。要教数学就需要突出这个意义上的数学。因此，要有粗糙的问题，供学生来练习抽象化——把实际问题转变成一个数学问题——的过程，而不是那种一个水龙头进入一个出水的应用题。甚至当我们把问题转化成一个明确的数学问题之后，我们可以利用计算机程序来帮我们求解。这样，我们就可以把更多的精力放在体会“数学是语言，数学是结构”上面。如果还能够结合实际问题，真的让学生体会自己的抽象和计算的结果发挥作用，那就更牛了。这才是数学。

当然，你可以继续问我，那到底教什么怎么教？我可以一个一个给你举具体的例子。但是，首先，教学要思考教什么怎么教，而不是照着教材或者什么东西教；其次，数学来说，需要按照上面的指导思想——数学是语言，数学是结构——来决定教什么怎么教；再次，每一个具体的数学内容，例如函数，例如微积分，例如矢量空间，都有属于自己的最核心的思想，教学要体现这些具体内容的核心思想。例如，线性代数最核心的不是行列式的计算不是求解线性方程，而是矢量空间的概念以及矩阵谱分解。我们需要思考为什么这些是核心，知道这些是核心以后教什么，怎么教，结合什么样的现实生活或者其他学科的例子。

认识不到需要思考“教什么，怎么教”就不能去搞教育，认识不到“数学是语言，数学是结构”就不能去当校长教研员，有了认识决定不了教什么想不出来怎么教就不能去当数学老师。当然，当老师的要求最高，这三个层次都得够格才行。

那为什么要把大家都培养成能够用数学来思考和描述世界或者至少体验过用数学来思考和描述世界的人呢？因为我们现在的时代已经不再是纯粹工业化的时代了，我们需要发挥每一个个体的创造性和创造性地解决问题的能力。如果仅仅是为了能够把某个其他人已经解决的问题而且有解决方式供参考的问题来解决掉，那么，我们不需要太多创造性，模仿即可。但是，一个模仿的人的模仿对文明的推动和一个创造性地提出来别人没有提出来过的问题的提出和，或者求解出来被人没有解决过的问题的解决，是不能相提并论的。我们已经到了一个需要发现和发挥每一个个体的创造性的时代了。博学、会算（比如比《最强大脑》赛事还强的20位数乘法）顶个屁用，有用的是发现问题和解决问题，有用的是运用知识和信息的能力。当然，你可以说如果都不知道这些知识如何会用啊。有这么一丁点道理，但是不能为了这一定点道理，就非得学会5分钟内做完20个微分或者积分或者20位数的乘法啊。

每次，我都让我的量子力学的学生跟我一起再一次发明“量子力学”的概念体系，然后跟实验对比，甚至尝试着发明一下别的理论试试。这样的尝试着自己构建，才是学习，而不是照着某个配方抓药。