课程名称: 线性代数
英文名称:Linear Algebra
【先修课要求】高中数学。推荐已经学习过一门编程语言(随着课程学习也可以),学过集合和映射方面的知识、数学建模方面的知识就更好了,但是不做要求。
【学生预计课程所花时间,小时,按照课程成绩良好以及以上学生粗糙估计】32(上课)+ 80(看书完成作业)+ 30(课程项目)+10(复习和考试)= 152。平均每周大约10小时。
课程简介
线性代数的矢量和矩阵为描述世界提供了具有一定普适性的数学结构,数值线性代数是最重要的数值计算方法。本课程主要包含四个模块的内容:矢量空间,矩阵论,数值线性代数,线性代数的应用案例。本课程也为物理学、系统科学、数值计算的多门课程提供知识上的基础。
课程目标
这门课程的知识上的目标是帮助学生建构从集合映射到线性空间的数学概念体系,以及学会做数值线性代数。同时,在本课程在思维方式上的目标是把问题抽象和转化成矩阵和矢量的问题的能力,依赖抽象概念展开思考的能力。注意,大量的对象都可以被抽象为矢量和矩阵以及张量等数学结构。因此,本课程的知识内容尽管从数学上就是矢量、矩阵、张量,但是在应用上,会通过例子展示其普适性和威力。顺便,本课程也会通过应用部分的例子来稍微展示一下线性代数和系统科学学科联系。
课程设计思想
本课程的设计原则是:按照课程目标来决定授课内容和授课方式,内容要体现这个学科的学科大图景——典型对象、典型问题、典型思维方式、典型分析方法、和世界还有其他学科的关系。
这个原则背后的理念是:学习是为了创造知识、创造性地使用知识、欣赏知识的创造和创造性的使用。为了这个目的,不仅仅要学会知识,有系统的知识,还要从知识的学习、知识的创造过程的学习中体会到如何创造知识和创造性地使用知识,也就是学科大图景。
本课程的设计方法是:绘制学科概念地图,包含基本概念、核心概念,概念之间的联系,以及概念和学科大图景的联系。以学科概念地图为基础选择所要教授的概念和概念关系,以及回答每一项所选择的内容的理据性——尤其是从研究工作以及概念依赖关系的角度的理据性,也就是为什么这些内容是值得学习的。具体设计过程,除了课程整体概念地图,就不在这里给出。
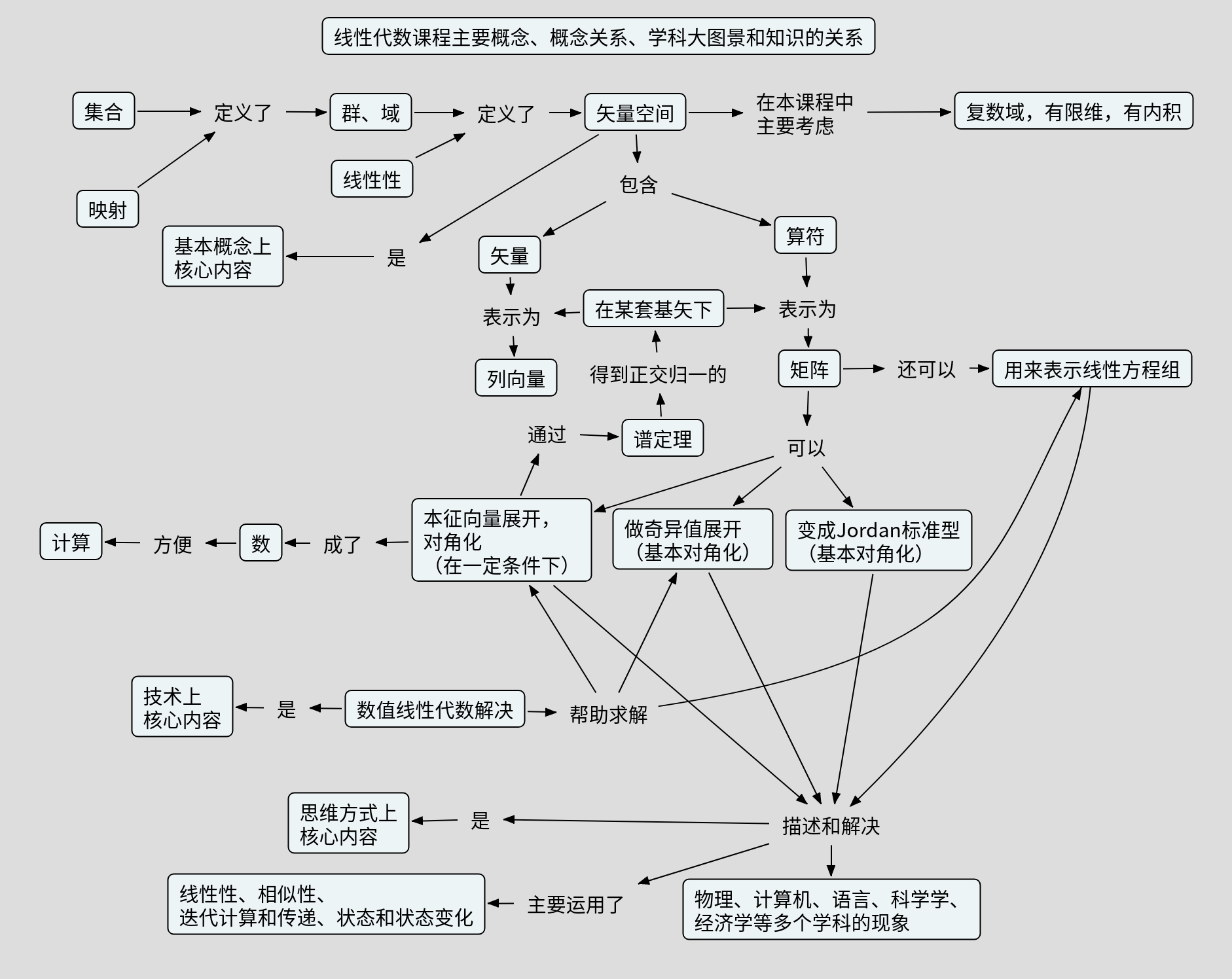
图1:《线性代数》主要概念、概念关系、学科大图景(课程目标)。
课程目标:线性代数给描述世界提供了最重要的数学结构,数值线性代数是最重要的数值计算方法。因此,这门课程的知识上的目标是帮助学生建构从集合映射到线性空间的数学概念体系,以及学会做数值线性代数。同时,在本课程在思维方式上的目标是把问题抽象和转化成矩阵和矢量的问题的能力,依赖抽象概念展开思考的能力。注意,大量的对象都可以被抽象为矢量和矩阵以及张量等数学结构。因此,本课程的典型对象尽管从数学上就是矢量、矩阵、张量,但是在应用上,要通过例子展示其普适性和威力。顺便,本课程也会通过应用部分的例子来稍微展示一下线性代数和系统科学学科联系。
按照这个目标所设计的本课程的四个模块是:矢量空间,矩阵论,数值线性代数,线性代数的应用案例。传统的以行列式和行列式的计算,尤其是手动计算,为基本目标的线性代数是完全不能实现上面的目标的。
另外,从教学方法上来讲,本课程采用的教学方法包含理解型学习、以项目为基础的学习、创造体验式学习、讲给别人听(同伴教学法)。这需要学生已经具有或者说能够被培养出来一定的自学能力,愿意投入时间去思考和完成课程项目和作业。大量的阅读材料和研究实例,以及学生在课后对阅读材料和研究实例的整理——制作反映学生理解和思考的概念地图,以及在此基础上完成课程项目。这门课程的缺点是:对学生的理解力要求比较高,对学生的时间投入要求比较高,对学生的学习动机也有要求。对学术感兴趣的学生可以从中学到更多东西。
培养学生的学习能力,帮助学生学会知识的同时学会学科思维方式体会好学科大图景,同时需要学生的时间和思考深度的投入是本课程的特点。如果这些不是你的目标,或者你觉得做不到要求的时间和思维深度,请不要选择本课程。
教学内容和学时分配
- 第零章 课程目标和学习方法(3学时,选修)
- 0.1 课程基本目标:知识目标和思维方式目标
- 0.2 理解型学习方法和概念地图
- 0.2.1 批判性思维和成长型思维
- 0.2.2 系联性思考
- 0.2.3 学科大图景
- 0.2.2 概念地图和概念地图的制作
- 0.3 科学、数学与现实的关系
- 0.3.1数学作为语言
- 0.3.2 数学作为结构
- 0.3.3数学建模
- 0.3.4 科学的实用主义和科学的可证伪性
- 0.3.5 归纳与演绎的逻辑
- 第一章 矢量空间(3学时讲授)
- 1.1 集合映射
- 1.2 群和域
- 1.3线性性和线性空间、线性空间上的算符
- 1.4 内积、矢量空间和对偶矢量空间
- 1.5 厄米算符谱定理、算符和矢量的表象理论和Dirac符号
- 第二章 矩阵论(10学时讲授+1学时习题课)
- 2.1 矩阵的本征值和本征向量
- 2.2 矩阵的奇异值分解
- 2.3矩阵的逆和广义逆
- 2.4 矩阵的迹和行列式
- 2.5 Jordan标准型
- 2.6 矩阵微扰论
- 2.7 Perron–Frobenius定理
- 第三章 数值线性代数(3学时讲授+1学时习题课)
- 3.1 矩阵相乘的Strassen算法
- 3.2 本征值问题的求解
- 3.3线性方程的解
- 3.4 子空间迭代求解
- 3.5数值线性代数系统
- 第四章 线性代数应用(8学时讲授+3学时课程项目报告,按照学生情况选学其中几个,其他当做课程项目)
- 4.1 矢量和量子力学
- 4.2 矢量和自然语言处理
- 4.3 矩阵和网络谱理论
- 4.4 矩阵、Markov过程、PageRank算法
- 4.5 矩阵和投入产出分析
- 4.6 矩阵和Ising模型
- 4.7 矩阵奇异值分解和主成分分析(PCA)
- 4.8 矩阵微积分和机器学习
- 4.9 矩阵和非线性动力学
- 4.10 矩阵和控制论
没有经过我自己的理性检验(观察实验或者计算推理)的东西不能成为我下一步思考和认识世界的基础。举例:平面几何(论证中每一个步骤都需要理由,都可能不成立)、伽利略关于“重物落的快”的论证(不是结论对就是对的,或者论据对就是对的,不是大人物说的就是对的,通过替换对象来考察隐藏的逻辑假设以及凸显事物的本质特征)
成长型思维:做中学、教中学、挑战着学、创造中学、任何时候都可以再进步。
未知联系已知就是理解,构建理解的基础和框架,具有系统性(核心和成长),和逐条记忆检索相反。注意,把联系表达成网络和矩阵之后,还可以分析和计算联系:系联=联系1+联系2+联系3+⋯,从孤立到有联系,从直接联系到间接联系,从个体到整体
一个学科的典型研究对象、典型研究问题、典型思维方式、典型分析方法、和世界还有其他学科的关系。
思考的语言,集合、映射的语言的重要性
举例:“苹果的加法运算”到底是定义在哪一个集合上的运算:苹果的集合、苹果数量的集合、还是幂集
从事物中抽象出关系,把关系整理成为数学结构,找到一个事物自身最切合的数学结构
举例:位置坐标存在加法运算吗,还是位移矢量?矢量加法的一般性和举例
举例:交换律不满足的操作(翻转三角形),矩阵
给事物的状态,事物的状态的变化——也就是状态上的操作,找最合适的数学结构
举例:位移的矢量模型,运动物体的质点模型
举例:最优编码与信息熵:概念是从现实世界里抽象出来的
科学为现实提供了可计算的可证伪(但是迄今为止还没有被证伪的)心智模型
归纳的作用和局限,天下乌鸦一般黑,归纳当做概率性推理
Lapack、Petsc、Slepc等求解本征值、奇异值、线性方程的解,并行程序设计
矢量描述量子系统的状态,矩阵是算符,Green函数和矩阵
矢量表示词汇、句子、段落、知识等语言单位
网络邻接矩阵和其他矩阵的本征值或者奇异值和网络结构的关系
Perron–Frobenius定理,Markov随机过程,不变分布
从直接投入产出系数到间接投入产出系数,矩阵微扰论用于投入产出分析
Ising模型的转移矩阵求解
取少数几个本征矢量或者奇异值矢量的近似
不动点附近的线性稳定性分析
教材与学习资源
教材:
Sheldon Axler《Linear Algebra Done Right》
吴金闪《系统科学导引》
参考书:
W.I.B. Beveridge, 《The Art of Scientific Investigation》
Karl Popper 《The Logic of Scientific Discovery》
Timothy Gowers,《Mathematics: A Very Short Introduction》
Albert Einstein and Leopold Infeld,《The Evolution of Physics》
Richard Feynman, 《The Character of Physical Law》
Richard Feynman,《The Feynman’s Lectures on Physics, III》
吴金闪《教的更少,学得更多》
吴金闪 《二能级体系上的量子力学》
五、考核方式
课程考核包括以下几项:
(1)作业(50%)
(2)课程项目(10%)
(3)期末闭卷考试(40%)
大纲起草人:吴金闪