这是小学数学教材上关于长方形和正方形的定义:
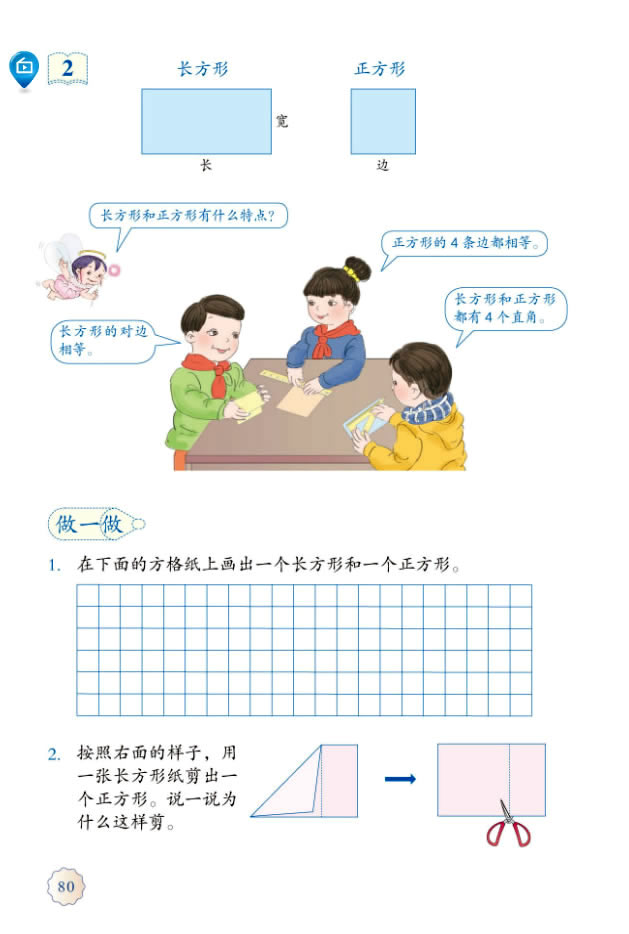
这里是课后练习(主要看第二题):
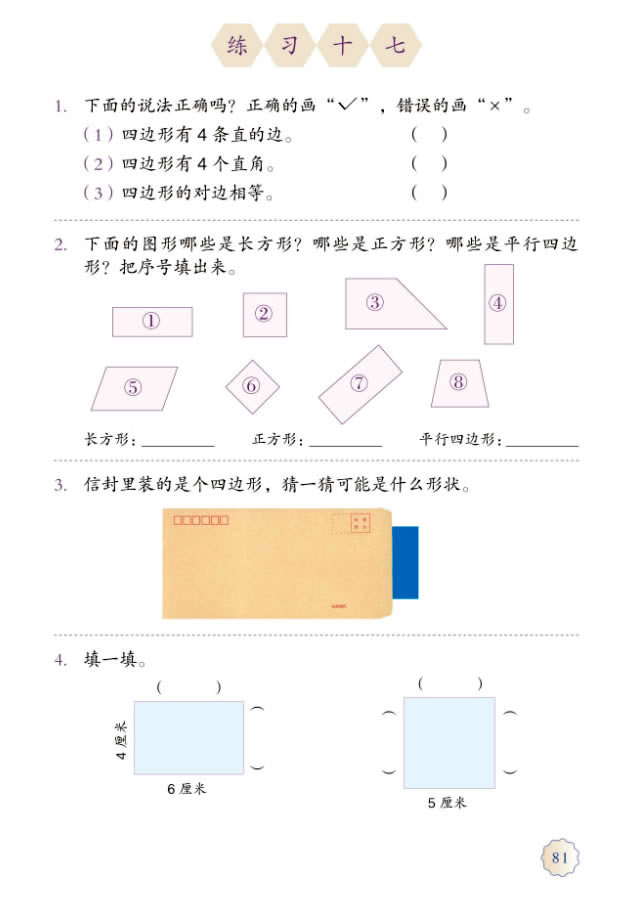
这个是老师给的答案:

听说不仅仅一两位老师给的答案是这个,很多很多老师都给的合格答案。所谓的教研员也要求老师按照这个答案来讲。
我特别想知道,教学参考书里面的答案是什么。如果教参就是这样,那这个板子不能主要打在老师身上,教材编写砖家们应该负主要责任。如果不是,那么,我想知道这些老师和教研员的理由是什么。在那之前,我只好猜测着做分析。下面就是猜测。
首先,从数学上,没有讨论的余地:平行四边形的概念包含长方形的概念,长方形的概念包含正方形的概念。这个就算去套定义,例如“正方形四边相等,四个角都是直角”,“长方形对边相等,四个角都是直角”,也可以得到,“四边相等”必然导致“对边相等”,因此,正方形必然是长方形。
那,为什么小学老师会坚持前面答案里面的教法呢?有的人甚至说,在中学阶段,正方形是长方形的特例,但是在小学阶段不是的。怎么会产生这样的答案呢?如果不可能向学生说明白,则万不得已的时候可以说“是特殊情况,但是,你们暂时还听不懂,中学再说”。可是,前面的逻辑完全没有说不明白的地方啊。那,到底怎么回事?为什么会有这么多的人坚持这样教?
我认为,有两个方面的直接因素:教条主义和不做理解型学习和教学,以及一个更加深刻的间接因素:不反思,没有批判性思维,以及一个能力方面的问题:没有整体数学观和科学观,也就是不懂得什么是数学什么是科学。
教条主义就是这个意思:担心一旦学生面对考试,如果出现了教材里面没有直接明明白白白纸黑字写下来的东西,有可能会被判错。因此,本着对学生负责(其实是对学生的考试成绩负责)的态度,上课只能教教材里面明明白白写下来的。而且,很多时候,要细扣到底写下来什么,要尽量发现“愿意”,尽量忠实于这个原意。至于实际上在学科上是什么意思,是不重要的,考试又不是考实际上这个学科上这个问题怎么看,而是,考教科书上怎么说。
教条主义和不做理解型学习,以及不明白这个学科本身是什么,是联系在一起的。只要做一个逻辑关系图,就很容易发现,正方形是长方形的特例。没什么可讨论的。当然,一部分老师我猜也明白,但是架不住“教条”啊,于是就会出现说中学可以是这样,但是,小学不能是这样的说法。
取消教材,变教材为参考书而且要多本一起使用,要教材列出来参考文献,让学科领域专家主持教材编写教学专家辅助,提高中小学老师的水平达到学科专家的层次(仅仅是研究能力上可能差点,对学科的认识要差不多在一个层次),在中小学老师中推广理解型学习和教学,用批判性思维和系联性思考武装中小学老师,这样才能解决问题。按照老师们的讨论,加上一条一般性的解决方案:教学参考书(教师用书)中应该针对这样的问题给出来从学科角度出发的认识和处理的可能的方式和理由,不能回避问题。
收到了一些老师的意见:第一、真的不知道这个包含关系的是少数老师。第二、由于某些原因,例如认为小学三年级不太能够搞清楚逻辑上的包含关系,或者习惯了这样教这样考,或者害怕孩子们考试的时候考虑了包含关系的答案会被判错,就还是坚持这个问题的答案就是这样。
收到了编辑的编写意图:小学三年级没有明确讲包含关系,因此两种答案都可以,但是考虑了包含关系的答案更好。
知道了老师们的意见以及编者的意图以后,我们来思考下面几个问题。第一,怎么办?显然,正确的答案应该是考虑了包含关系的那个,这个看起来差不多是共识。那么,怎么办,这个题怎么回答,老师上课怎么教?处理方法之一,可以避开这个问题,也就是说,请编者取消这个问题。如果要问,不要把三个形状放在一起问,一个一个问。而且,在分开问的问题中,也要注意给出来的形状不要“启发”或者“诱导”学生展开三者关系的思考,也就是说,在问长方形的问题中,不要出现正方形。当然,这不是一个好办法,但是可以接受——要么不讲,要么讲清楚讲对。这个方式就是不讲。处理方法之二,就是讲清楚,而且讲清楚还有助于学生展开理解型学习(系联性思考和批判性思维)。用一位老师的话来说是这样的:
追根溯源,“唯教材”“唯标准答案”还是根源。事实上,只是理解了”上位学习“与”下位学习“这些基本心理学原理,就知道应该循序渐进引导学生进行归纳与提炼。先学正方形,后来学了长方形之后可以归纳进去;再学了平行四边形之后还可以继续归纳。学习菱形之后,就可以对比分析,从异与同的比较中深化理解。
一方面教材编写者在提供给一线教师的指导用书里要针对这些情况做具体的指导与说明,让一线教师理解教材编写者其实是这样思考的,学科中应该如此理解;另一方面就是要通过研训引导教师能够从学科本质出发去从事真的教学,鼓励一线教师敢于表达自己的观点,不要唯“标准答案”。
希望这个解决方案能够解决“正方形是不是长方形”这个具体问题。
解决了怎么办的问题,假设真的能够按照上面的方式来解决来实现的话,我们来追问为什么的问题,为什么会产生这样的习惯?这位老师也提到了“唯教材”、“唯标准答案”。可是,教材上没有规定一定要不考虑包含关系的才是标准答案啊,编者的意图也不是这样(假设我收到的编者意图具有代表性的话)啊。那这个习惯到底来自于哪里?至少现在,我不是很清楚真正的来源。搞清楚这个问题是很有意义的。我们就有希望搞清楚教学中“教条主义”的来源或者说堡垒。是不是有可能是教研员群体,还是某一次高考中考或者什么考试的结果?谢谢老师们的讨论。很有意义。希望老师们继续帮我寻找这个为什么的答案。真心不希望中小学教育的内容是和学科知识学科精神脱离的另一套自成体系的东西。
有这样一群勇于分析自己的老师,我们就还有希望。